Problem
Sie müssen bestimmen, ob eine Zahlenfolge mit einem Stapel sortiert werden kann.
Ein Zug fuhr von Gleis 1 aus in eine Sackgasse (siehe Abbildung). Es ist erlaubt, einen oder mehrere der ersten Wagen vom Zug abzuhängen und in eine Sackgasse zu bringen (falls gewünscht, können Sie sogar den gesamten Zug gleichzeitig in eine Sackgasse bringen). Danach wird ein Teil der Waggons in Richtung Gleis 2 abtransportiert. Dann können Sie ein paar weitere Wagen in die Sackgasse bringen und wieder einen Teil der Wagen in Richtung Gleis 2 transportieren. Und so weiter, damit jeder Wagen nur einmal von Weg 1 in eine Sackgasse fährt und dann einmal aus der Sackgasse auf Weg 2 fährt. Das Einfahren in eine Sackgasse von Weg 2 oder das Ausfahren aus einer Sackgasse auf Weg 1 ist verboten. Es ist unmöglich, von Weg 1 auf Weg 2 zu gelangen, ohne in eine Sackgasse zu geraten.
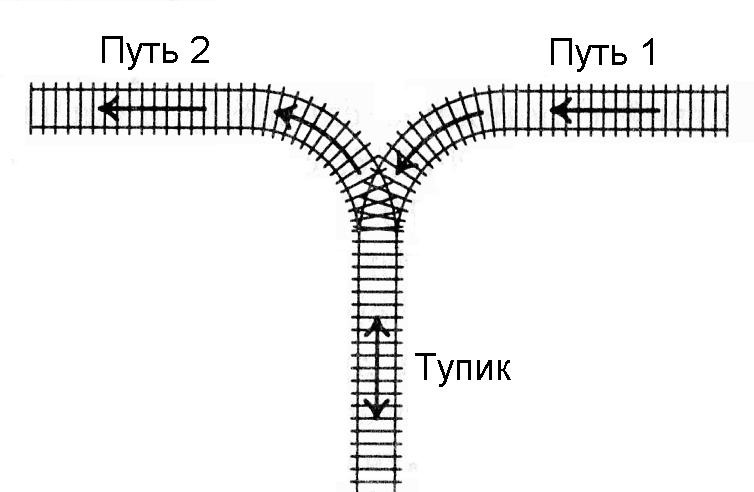
Es ist bekannt, in welcher Reihenfolge die Züge anfangs fahren. Es ist erforderlich, mit Hilfe dieser Operationen sicherzustellen, dass die Wagen des Zuges in Ordnung sind (zuerst der erste, dann der zweite usw., wobei vom Kopf des Zuges, der auf dem Weg 2 in Richtung der Sackgasse fährt, gezählt wird). Schreiben Sie ein Programm, das bestimmt, ob dies möglich ist.
Eingabe
Sie geben die Zahl N ein (\(1<=N<=2000\)). Als nächstes kommen die Wagennummern in der Reihenfolge vom Kopf des Zuges, der auf dem Weg 1 in Richtung Sackgasse fährt. Die Wagen sind mit natürlichen Zahlen von 1 bis N nummeriert, die jeweils genau einmal vorkommen.
Ausgabe
Ist es möglich, dass die Wagen von 1 bis zu N in Ordnung sind und vom Kopf des Zuges gezählt werden, wenn der Zug aus einer Sackgasse auf Gleis 2 fährt? Wenn Sie können, geben Sie YES aus. Wenn dies nicht möglich ist, geben Sie NO aus.
Beispiele
| № |
Eingabe |
Ausgabe |
Hinweis |
| 1 |
3
3 2 1 |
YES |
Man muss den ganzen Zug in eine Sackgasse bringen und ihn dann komplett auf den 2. Weg bringen |
| 2 |
4
4 1 3 2
|
YES
|
Zuerst müssen Sie zwei Autos in eine Sackgasse bringen, von denen einer in einer Sackgasse bleibt, und dann den zweiten Wagen in eine Sackgasse bringen, dann zwei weitere Wagen in eine Sackgasse bringen und 3 Autos, die in einer Sackgasse stehen, auf die 2. Straße bringen |
| 3 |
3
2 3 1 |
NO |
|