Problem
Asya liebt Tiere sehr. Sie hat vor kurzem n Kätzchen gekauft, ihnen numerische IDs von 1 bis n gegeben und sich in einer Voliere niedergelassen. Die Voliere ist eine Reihe von n Zellen, die ebenfalls von 1 bis n nummeriert sind. Die benachbarten Zellen sind durch Netzscheidewände getrennt, insgesamt gibt es in der Voliere n−1 Trennwände. Anfangs hat sich genau ein Kätzchen mit einer bestimmten Nummer in jeder Zelle niedergelassen.
Als sie die Kätzchen beobachtete, bemerkte Asya, dass sie sehr freundlich waren und einige Paare, die in benachbarten Zellen lebten, sehr bereit waren, miteinander zu spielen. Um ihnen dieses Vergnügen nicht zu nehmen, nahm Asya die Trennwände zwischen den benachbarten Zellen heraus und machte sie größer.
Am ersten Tag machte Asya Folgendes.
Ich habe darauf hingewiesen, dass einige Kätzchen x
i und y
i, die am ersten Tag in benachbarten Zellen leben, spielen wollen.
Sie entfernte die Trennwand zwischen diesen Zellen und verwandelte sie in eine, in der sich alle Kätzchen aus den beiden früheren Zellen befanden.
Da Asya keine Trennwände zurückgab, wurde die Voliere nach n−1 Tag zu einer einzigen Zelle, in der alle Kätzchen lebten. Da sie sehr pedantisch war, schrieb Asya für jeden der n−1 Tage die IDs der Kätzchen x
i und y
iin ein spezielles Protokoll ein.
Sie haben ein Protokoll mit diesen Informationen in die Hände bekommen, aber Sie wissen nicht, wie die Kätzchen ursprünglich in den Zellen angesiedelt waren. Finde jede Ansiedlung von Kätzchen in n-Zellen, die den Daten in der Zeitschrift nicht widerspricht.
Eingabe
Die erste Zeile enthält eine ganze Zahl n (
\(2 \leq n \leq 150000\)) — Anzahl der Kätzchen.
Die folgenden n−1 Zeilen enthalten ganze Zahlenpaare x
i, y
i(
\(1 \leq x_i, y_i, \leq n,x_i \neq y_i\) ) Die IDs der Kätzchen, zwischen denen die Trennwand am Tag i entfernt wurde. Es ist garantiert, dass die xi-Kätzchen am Tag i entfernt wurden. und yi befinden sich nicht in derselben Zelle nach den Ergebnissen früherer Zellverknüpfungen.
Ausgabe
Geben Sie n verschiedene ganze Zahlen aus p
i (
\(1 \leq p_i \leq n\)), wobei p
i die ID des Kätzchen ist, das ursprünglich in der Zelle mit der Nummer i gelebt hat. Wenn es mehrere mögliche Antworten gibt, geben Sie eine von ihnen aus.
Hinweis
Die Antwort zeigt zum Beispiel eine der möglichen ursprünglichen Siedlungen von Kätzchen, es gibt andere Antwortmöglichkeiten. Das folgende Bild zeigt, wie die Zellen für diese Variante der ursprünglichen Platzierung von Kätzchen zusammengeführt wurden. Beachten Sie, dass sich Kätzchen, die sich an jedem Tag gemäß dem Asi-Protokoll angefreundet haben, bei dieser Platzierung in benachbarten Zellen befinden.
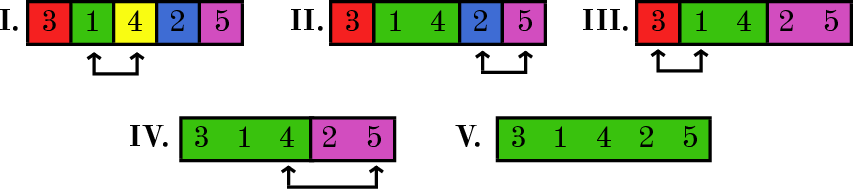
| Eingabe |
Ausgabe |
5
1 4
2 5
3 1
4 5 |
3 1 4 2 5 |