Suche tief.DFSErkennung tief. DFS) ist einer der Hauptalgorithmen auf den Zählungen. Algorithm arbeitet für O(N + M)♪ AlgorithmenFür Anfänger beginnen wir von oben, schauen uns die Kinder dieses Tops an, und wenn wir nie reingekommen sind, fangen wir mit ihnen an. DFS♪ 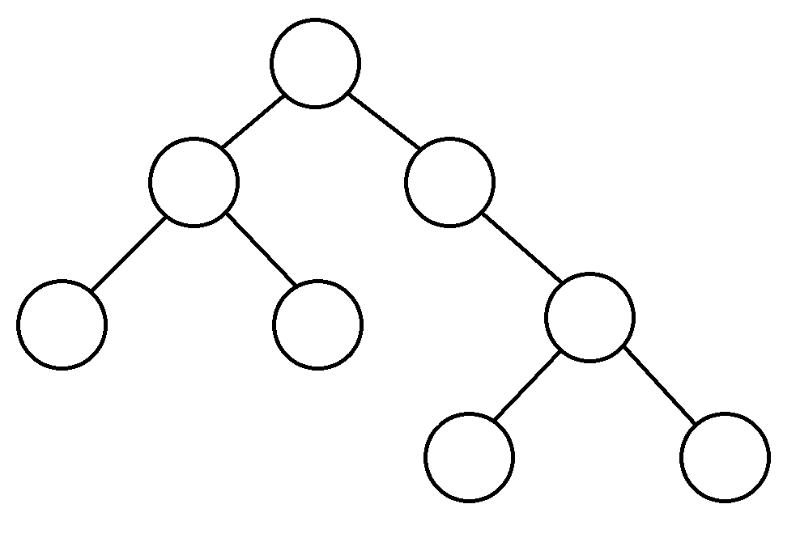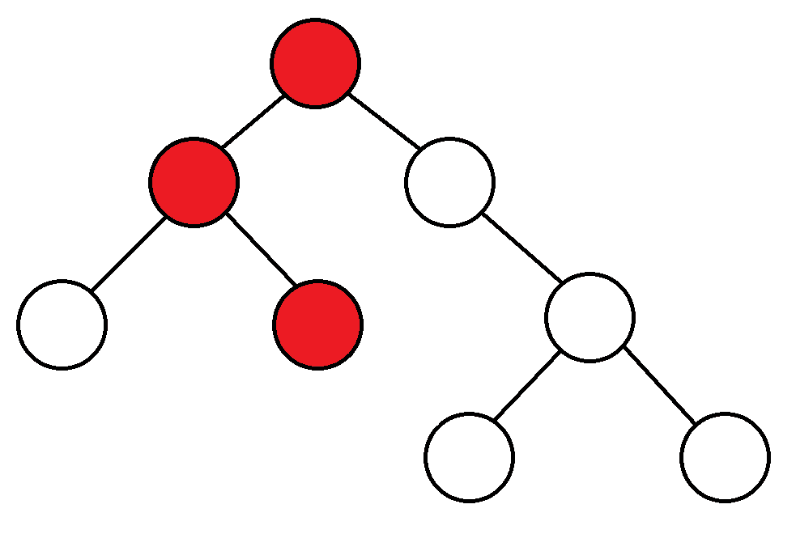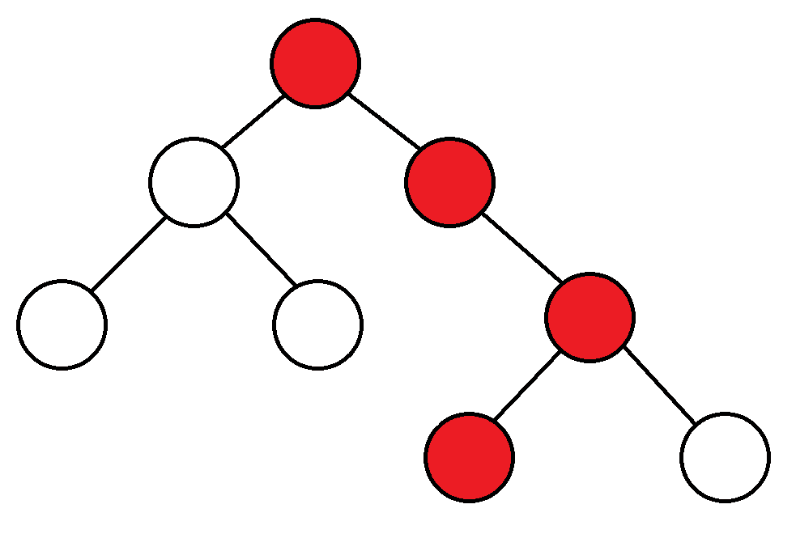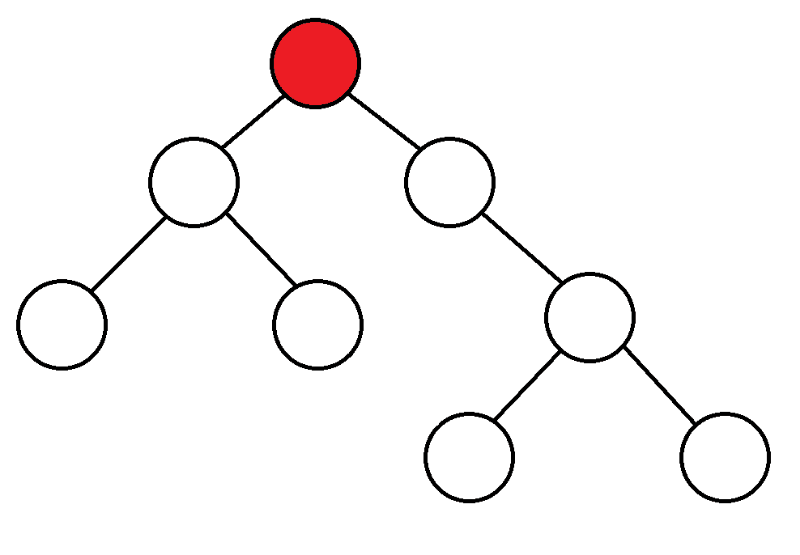
|
Suche tief.DFSErkennung tief. DFS) ist einer der Hauptalgorithmen auf den Zählungen. Algorithm arbeitet für O(N + M)♪ AlgorithmenFür Anfänger beginnen wir von oben, schauen uns die Kinder dieses Tops an, und wenn wir nie reingekommen sind, fangen wir mit ihnen an. DFS♪ 
|
Dwood CountDwood Count - eine Reihe, deren Spitzen in zwei Multipliken zerbrochen werden können, so dass jede Rippe die Oberseiten verschiedener Multiplikationen verbindet.
Das Konzept wird häufig im Kontext von Doppel-Doppel-Diagrammen verwendetFarbeOben. Die Aufteilung der Zählung in zwei Proportionen wird genanntUkraineSein Top ist zwei verschiedene Farben. Jede Rippe muss die Oberseiten verschiedener Farben verbinden.
Um die Doppeldoppelung zu überprüfen und die Probe nach Maß zu kalibrieren, am häufigsten verwendet DFS♪
AlgorithmenBeginnen wir eine Farbe mit einer beliebigen Spitze, die in einer beliebigen Farbe lackiert ist.
Wenn wir durch jede Rippe gehen, malen wir das nächste Top in der entgegengesetzten Farbe.
Wenn wir einen Peak von benachbarten Peaks gefunden haben, die bereits in der gleichen Farbe wie die aktuelle, gibt es einen ungeraden Zyklus in der Zählung, was bedeutet, dass es nicht zwei-Wege ist.
|
Der Algorithmus kann wie folgt beschrieben werden:
Dun ist eine Zielzahl mit n Tops und m Rippen. Es ist notwendig, sein Oberteil umzunummerieren, so dass jede Rippe von oben mit einer geringeren Anzahl nach oben mit einer größeren Anzahl angetrieben wird. Mit anderen Worten, es besteht die Notwendigkeit, nach der von allen Zählrippen festgelegten Reihenfolge nach oben (topologische Reihenfolge) zurückzukehren.
Wir verwenden Bypass in der Tiefe (dfs(v)) Wenn wir hier verschwinden.- Ja.Hinzufügen unserer Spitze zu Beginn einer Liste, es wird schließlich eine Topologie Sortierung sein. So Der Antrag auf Topologie ist eine Sortierung, um die Zeit der Ausfahrt zu verlieren.
|