DFS DFS
La recherche en profondeur d'abord ( DFS) est l'un des principaux algorithmes sur les graphes. L'algorithme s'exécute en O(N + M).
Algorithme
Pour commencer, nous partons du sommet, considérons les enfants de ce sommet, et si nous ne les avons jamais saisis, nous démarrons DFS à partir d'eux.
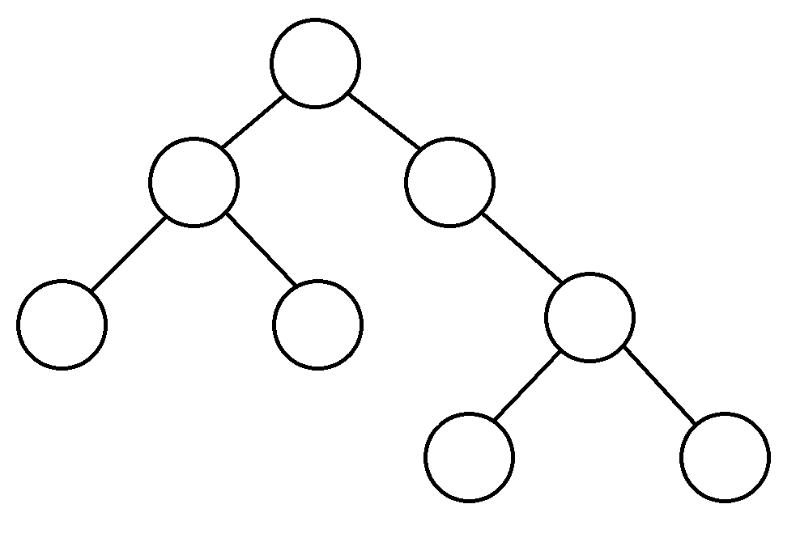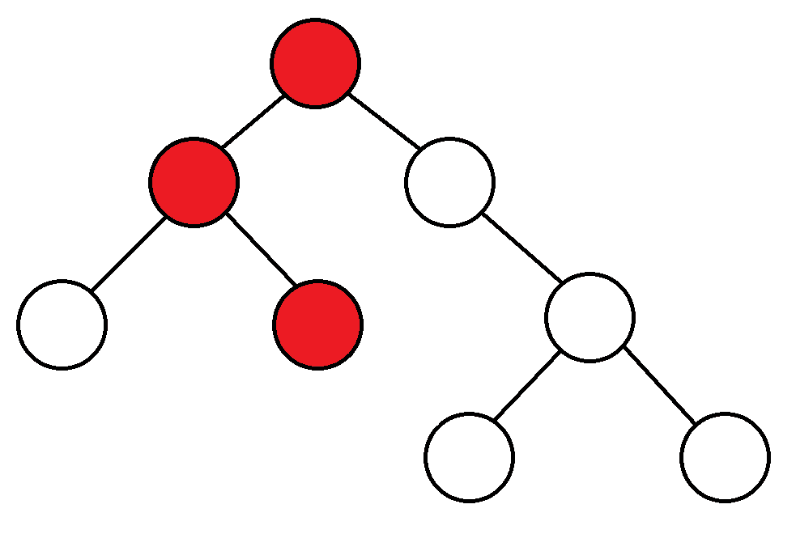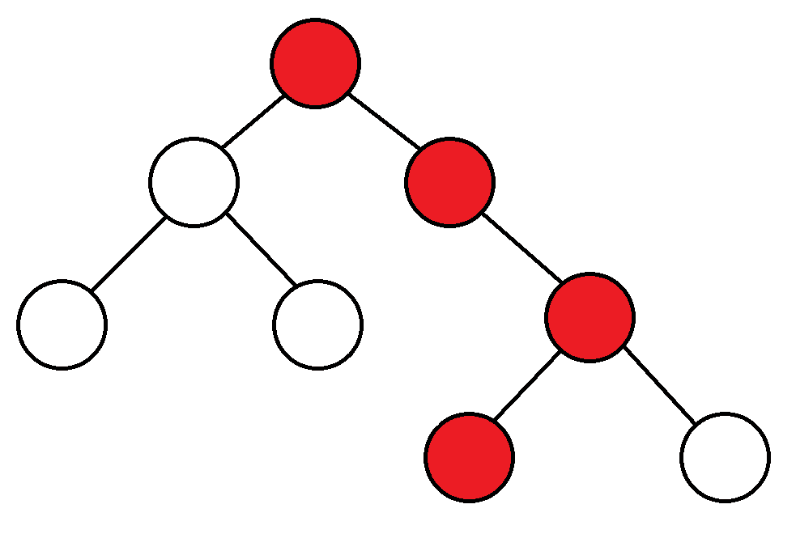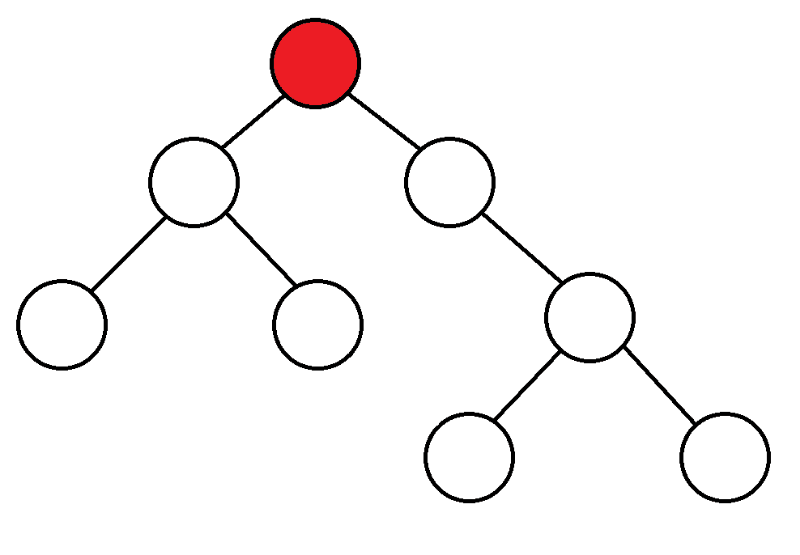
|
DFS DFS
La recherche en profondeur d'abord ( DFS) est l'un des principaux algorithmes sur les graphes. L'algorithme s'exécute en O(N + M).
Algorithme
Pour commencer, nous partons du sommet, considérons les enfants de ce sommet, et si nous ne les avons jamais saisis, nous démarrons DFS à partir d'eux.

|
Graphe bipartite
Graphe bipartite - un graphe dont les sommets peuvent être divisés en deux ensembles de sorte que chaque arête relie le sommets de différents ensembles.
Souvent, dans le contexte des graphes bipartis, le concept de couleurs sommets est utilisé. Diviser un graphe en deux parties s'appelle colorer ses sommets avec deux couleurs différentes. Chaque arête doit relier des sommets d'une couleur différente.
DFS.
Algorithme
Nous commençons à peindre à partir d'un sommet arbitraire, que nous peignons dans une couleur arbitraire.
En passant le long de chaque arête, peignez le sommet suivant dans la couleur opposée.
Si, en itérant sur des sommets voisins, nous trouvons un sommet qui est déjà peint de la même couleur que le sommet actuel, alors il y a un cycle impair dans le graphe, ce qui signifie qu'il n'est pas bipartite.
|
L'algorithme peut être décrit comme suit :
Soit un graphe orienté à n sommets et m arêtes. Il est nécessaire de renuméroter ses sommets de manière à ce que chaque arête mène d'un sommet avec un numéro inférieur à un sommet avec un numéro supérieur.
En d'autres termes, il s'agit de trouver une permutation de sommets (ordre topologique) correspondant à l'ordre donné par toutes les arêtes du graphe.
Nous allons utiliser la recherche en profondeur (dfs(v))
Si nous ajoutons notre sommet au début d'une liste au moment de la sortie de \(dfs(v)\) , alors à la fin dans cette liste vous obtenez un tri topologique.
Ainsi, le tri topologique souhaité — ceci est trié par ordre décroissant des heures de sortie.
|