Une procédure ou une fonction peut contenir un appel à une autre procédure en son sein. Y compris, le sous-programme peut s'appeler. Dans ce cas, l'ordinateur s'en fiche. Comme toujours, il exécute systématiquement les commandes qu'il a rencontrées de haut en bas.
Si vous vous souvenez des mathématiques, vous pouvez y rencontrer le principe de l'induction mathématique. C'est comme suit : une affirmation est vraie pour tout n naturel si
1) il est valable pour n = 1 ;
2) de la validité de l'énoncé pour tout naturel n = k il s'ensuit qu'il est vrai pourn = k+1.
En programmation, cette technique s'appelle la récursivité.
La récursivité est un moyen de définir un ensemble d'objets en fonction de l'ensemble lui-même, sur la base de cas de base simples donnés.
Récursif est une procédure (fonction) qui s'appelle elle-même directement ou via d'autres procédures et fonctions.
Exemple de procédure récursive :
vide Rec(int a)
{
si (a>0) { Rec(a-1); }
Console.WriteLine(a);
}
Schématiquement, le travail de récursivité peut être représenté sous forme d'organigramme.
Rec() la procédure est exécutée avec le paramètre 3 Ensuite, à l'intérieur de la procédure de paramètre 3, la procédure de paramètre 2 est appelée, et ainsi de suite, jusqu'à ce que la procédure de paramètre 0 soit appelée. Ensuite, le contrôle est renvoyé à la procédure avec le paramètre 1, elle termine également son travail en imprimant le numéro 1, et ainsi de suite. avant la procédure avec le paramètre 3.
Toutes les procédures appelées sont stockées en mémoire jusqu'à ce qu'elles terminent leur travail. Le nombre de procédures simultanées est appelé profondeur de récursivité.
|
Nous avons découvert que la récursivité est l'exécution répétée de commandes contenues dans une sous-routine. Et cela, à son tour, est similaire au travail du cycle. Il existe des langages de programmation dans lesquels la construction de boucle est absente du tout, par exemple Prolog.
Essayons de simuler le travail de la boucle pour.
La boucle for contient une variable de compteur de pas. Dans un sous-programme récursif, une telle variable peut être passée en paramètre.
// procédure LoopImitation() avec deux paramètres
// premier paramètre – compteur de pas, second paramètre – nombre total d'étapes
static void LoopImitation(int i, int n)
{
Console.WriteLine("Bonjour N" + i); // instruction à répéter pour toute valeur i
si (i < n) // jusqu'à ce que le compteur de boucle soit égal à n,
{
BoucleImitation(i+1, n); // appelant un nouveau procédure d'instance, avec le paramètre i+1 (aller à la valeur i suivante)
}
}
|
Récursivité et itération
Pour comprendre la récursivité, vous devez comprendre la récursivité...
Itération en programmation - une étaped'un processus de traitement de données cyclique.
Souvent, les algorithmes itératifs à l'étape en cours (itération) utilisent le résultat de la même opération ou action calculée aux étapes précédentes. Un exemple de tels calculs est le calcul des relations de récurrence.
Un exemple simple de valeur récursive est la factorielle : \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\).
Le calcul de la valeur à chaque étape (itération) est \(N=N \cdot i\) . Lors du calcul de la valeur de \(N\), nous prenons la valeur déjà stockée \(N\).< br />
La factorielle d'un nombre peut également être décrite à l'aide de la formule récurrente :
\(\begin{equation*} n != \begin{cases} 1 &\text{n <= 1,}\\ (n-1) ! \cdot n &\text{n > 1.} \end{cas} \end{équation*}\)
Vous remarquerez peut-être que cette description n'est rien de plus qu'une fonction récursive.
Ici, la première ligne ( \(n <= 1\)) est le cas de base (condition de terminaison de la récursivité) et la deuxième ligne est la transition vers l'étape suivante. < br />
| Fonction factorielle récursive |
Algorithme itératif |
static int Factoriel(int n){
si (n > 1)
return n * Factoriel(n - 1);
sinon retourner 1 ;
}
int x = 1 ;
pour (int je = 2; je <= n; je++)
x = x * je ;
Console.WriteLine("%d", x);
Il faut comprendre que les appels de fonction impliquent une surcharge supplémentaire, donc un calcul factoriel non récursif sera légèrement plus rapide.
Conclusion : où vous pouvez écrire un programme avec un algorithme itératif simple, sans récursivité, alors vous devez écrire sans récursivité. Mais encore, il existe une grande classe de problèmes où le processus de calcul est mis en œuvre uniquement par récursivité.
En revanche, les algorithmes récursifs sont souvent plus compréhensibles.
|
Traduction récursive d'un nombre d'un système de numération à un autre
Dans dans certaines situations, les procédures peuvent utiliser le mot return sans argument - c'est-à-dire qu'en fait, la procédure ne retourne toujours rien. Cela peut être utile lors de la récursivité, lorsque < code>return est utilisé pour terminer la descente aux cas de base des valeurs de paramètres en cours de récurrence. Par exemple, une procédure qui convertit un nombre décimal en binaire peut ressembler à ceci :
static void printTwo(int n)
{
si (n == 0) retour ;
printTwo(n / 2);
if (n % 2 == 0) Console.Write(0);
else Console.Write(1);
}
|
Tâche
Dans l'alphabet de la langue de la tribu "Tumba-Yumba" ; quatre lettres : "K", "L", "M" et "N". Vous devez afficher tous les mots composés de n lettres qui peuvent être construits à partir des lettres de cet alphabet.
Le problème est un problème normal de force brute qui peut être réduit à un problème plus petit.
Nous substituerons séquentiellement des lettres au mot.
La première position d'un mot peut être l'une des 4 lettres de l'alphabet (K. L, M, N).
Mettons la lettre K en premier. Ensuite, afin d'obtenir toutes les variantes avec la première lettre K, vous devez énumérer toutes les combinaisons possibles de lettres dans les positions n - 1 restantes et ainsi de suite. (voir photo).
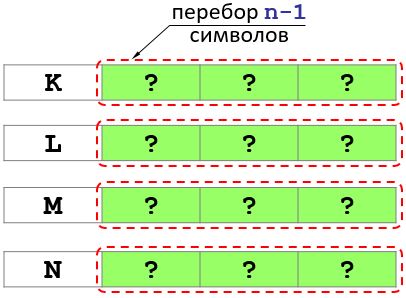 Ainsi, le problème se réduit à résoudre quatre problèmes de longueur n - 1.
Itérer sur n caractères de manière récursive
w[0]='K'; // itération sur les derniers L-1 caractères
w[0]='L'; // itération sur les derniers L-1 caractères
w[0]='M'; // itération sur les derniers L-1 caractères
w[0]='N'; // itération sur les derniers L-1 caractères
w - une chaîne de caractères qui stocke le mot de travail.
Ainsi, nous avons obtenu la récursivité. Nous pouvons organiser la solution du problème sous la forme d'une procédure récursive.
Reste à déterminer quand la récursivité prendra fin ? Lorsque tous les caractères sont définis, c'est-à-dire que le nombre de caractères définis est n. Dans ce cas, vous devez afficher le mot résultant à l'écran et quitter la procédure.
Le programme C# ressemblera à ceci.
// w - paramètre modifiable (string-result)
// La procédure TumbaWords reçoit l'alphabet sous forme de chaîne de caractères,
// le mot mot et le nombre de caractères déjà définis (au début – 0)
static void TumbaWords( string A, ref string w, int N )
{
if (N == w.Length) // w.Length - le nombre de caractères dans la chaîne
{
// si tous les caractères ont déjà été définis pour le mot,
// alors il faut sortir une chaîne et terminer la procédure
Console.WriteLine(w);
retour;
}
for ( int i = 0; i < w.Length; i ++ ) // si la condition ci-dessus est fausse (c'est-à-dire que tous les caractères ne sont pas espacés,
{
// si la condition ci-dessus est fausse (c'est-à-dire que tous les caractères ne sont pas espacés,
// puis dans la boucle on parcourt tous les caractères de l'alphabet et
// place alternativement le caractère sur la première case libre
w += A[i] ;
TumbaWords(A, ref w, N+1);
w = w.Remove(w.Length - 1); // puis supprimer le dernier caractère ajouté,
// pour créer un nouveau mot avec le même préfixe
}
}
vide statique Main()
{
int n = Convert.ToInt32(Console.ReadLine());
mot de chaîne = "";
TumbaWords("KLMN", mot de référence, 0);
}
NOTEZ que w est un paramètre modifiable (chaîne de résultat) !
|