DFS DFS
La prima ricerca in profondità ( DFS) è uno dei principali algoritmi sui grafici. L'algoritmo viene eseguito in O(N + M).
Algoritmo
Per cominciare, partiamo dall'alto, consideriamo i figli di questo top, e se non li abbiamo mai inseriti, allora iniziamo DFS da loro.
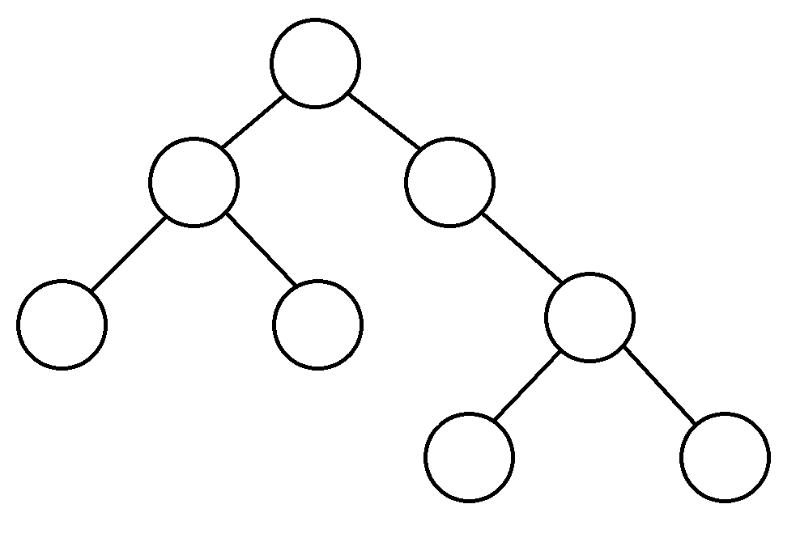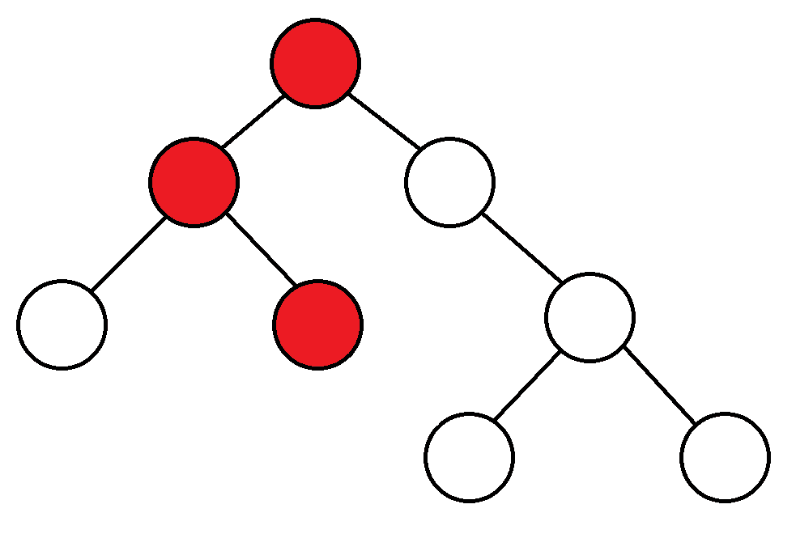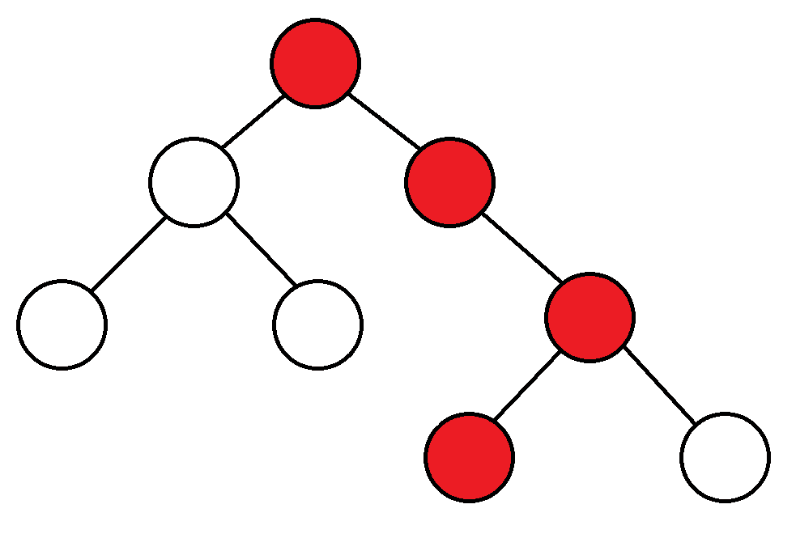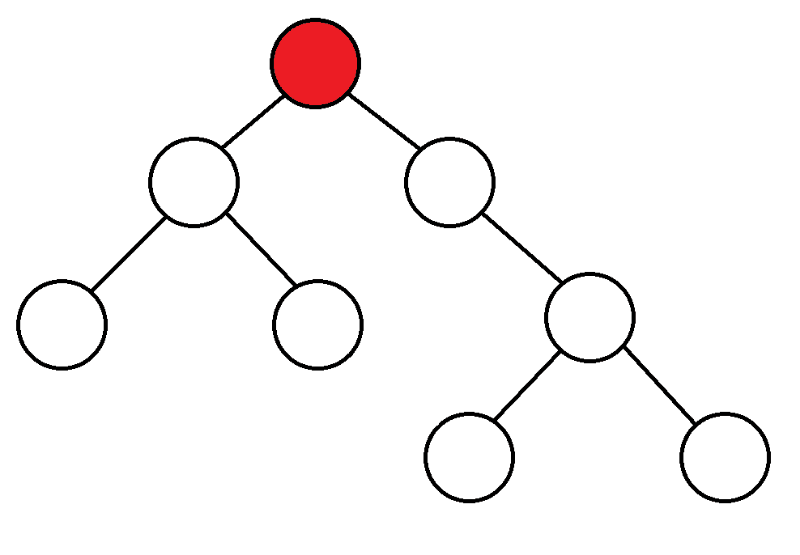
|
DFS DFS
La prima ricerca in profondità ( DFS) è uno dei principali algoritmi sui grafici. L'algoritmo viene eseguito in O(N + M).
Algoritmo
Per cominciare, partiamo dall'alto, consideriamo i figli di questo top, e se non li abbiamo mai inseriti, allora iniziamo DFS da loro.

|
Grafico bipartito
Grafico bipartito - un grafico i cui vertici possono essere divisi in due insiemi in modo che ciascun bordo colleghi il vertici da insiemi diversi.
Spesso nel contesto dei grafici bipartiti, viene utilizzato il concetto di colori vertici. Dividere un grafico in due parti si chiama colorare i suoi vertici con due colori diversi. Ogni bordo deve collegare i vertici di un colore diverso.
DFS.
Algoritmo
Iniziamo a dipingere da un vertice arbitrario, che dipingiamo con un colore arbitrario.
Quando passi lungo ogni bordo, dipingi il vertice successivo con il colore opposto.
Se, durante l'iterazione sui vertici vicini, troviamo un vertice che è già dipinto dello stesso colore di quello attuale, allora c'è un ciclo dispari nel grafico, il che significa che non è bipartito.
|
L'algoritmo può essere descritto come segue:
Dato un grafo orientato con n vertici e m archi. È necessario rinumerare i suoi vertici in modo tale che ogni bordo conduca da un vertice con un numero inferiore a un vertice con uno più alto.
In altre parole, è necessario trovare una permutazione di vertici (ordine topologico) corrispondente all'ordine dato da tutti gli spigoli del grafo.
Useremo la ricerca in profondità (dfs(v))
Se aggiungiamo il nostro vertice all'inizio di una lista al momento dell'uscita da \(dfs(v)\) , allora alla fine in questo elenco ottieni un ordinamento topologico.
Pertanto, l'ordinamento topologico desiderato — questo è ordinato in ordine decrescente di orari di uscita.
|