Problem
アシャは動物が大好きです。彼女は最近 n 匹の子猫を購入し、1 から n までの数字の識別子を付けて、囲いの中に入れました。鳥小屋は n 個のセルの列で、1 から n まで番号が付けられています。隣接するセルはメッシュ パーティションで区切られており、エンクロージャ内には合計で n & マイナス 1 のパーティションがあります。最初は、各セルに一定数の子猫が 1 匹だけ配置されていました。
子猫たちを観察していると、Asya さんは、彼らがとても友好的で、隣のセルに住んでいる子猫のペアが本当にお互いに遊びたいと思っていることに気付きました。この喜びを奪わないために、アシャは隣接するセルの間の仕切りを取り除き、セルを大きくしました。
i 日目に Asya は次のことを行いました。
私は、i 日目に隣のセルに住んでいる子猫 x
i と y
i が遊びたがっているのに気付きました。
これらのセルの間のパーティションを削除して、前の 2 つのセルのすべての子猫が 1 つになった.
アシャは仕切りを返さなかったので、n&マイナス1日後、囲いはすべての子猫が住む単一のセルになりました。非常に衒学的な Asya は、n−1 日ごとに x
i と y
i の子猫 ID を特別な日誌に書き留めました。
あなたはこの情報を掲載した雑誌を手に入れましたが、そもそも子猫がどのようにして独房に定着したかはわかりません。ログ内のデータと矛盾しない、元の n 個のセル内の子猫の分布を見つけます。
入力
最初の行には整数 n (
\(2 \leq n \leq 150000\)) — が含まれています。子猫の数。
次の n−1 行には、整数のペア x
i 、 y
i (
\(1 \leq x_i , y_i, \leq n,x_i \neq y_i\) ) — i日目にパーティションが削除されたセル間の子猫の識別子。以前のセル結合の結果、子猫 xi と yi が同じセルにないことが保証されます。
インプリント
n 個の異なる整数 p
i (
\(1 \leq p_i \leq n\)) を出力します。ここで p
i —最初にセル番号 i に住んでいた子猫の識別子。考えられる答えが複数ある場合は、そのうちのどれかを印刷してください。
注意
答えでは、例えば、子猫の可能な初期和解の1つが与えられ、他の答えがあります。下の画像は、この子猫の初期配置のためにセルがどのように結合されたかを示しています。この配置では、アーシャの日誌によると、毎日友達になった子猫は隣のセルにいることに注意してください。
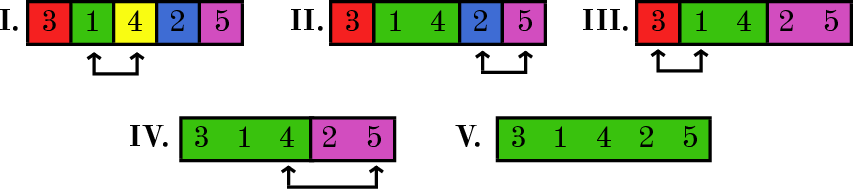
<本体>
| 入力 |
出力 |
5
14
25
3 1
4 5 |
3 1 4 2 5 |