シーケンスのハッシュを計算するだけでなく、その各プレフィックスに値を保存できます。これらは対応するプレフィックスと等しいシーケンスのハッシュ値になることに注意してください。
このような構造を使用すると、このシーケンスのサブセグメントのハッシュ値をすばやく計算できます (プレフィックスの合計と同様)。
サブセグメント [l;r] のハッシュを計算したい場合は、プレフィックス r のハッシュを取得し、プレフィックス l-1 のハッシュと p の r-l+1 乗を減算する必要があります。なぜそうなるのかは、プレフィックスに値を書き込んで何が起こるかを確認すると明らかになります。この写真を見て成功することを願っています
。
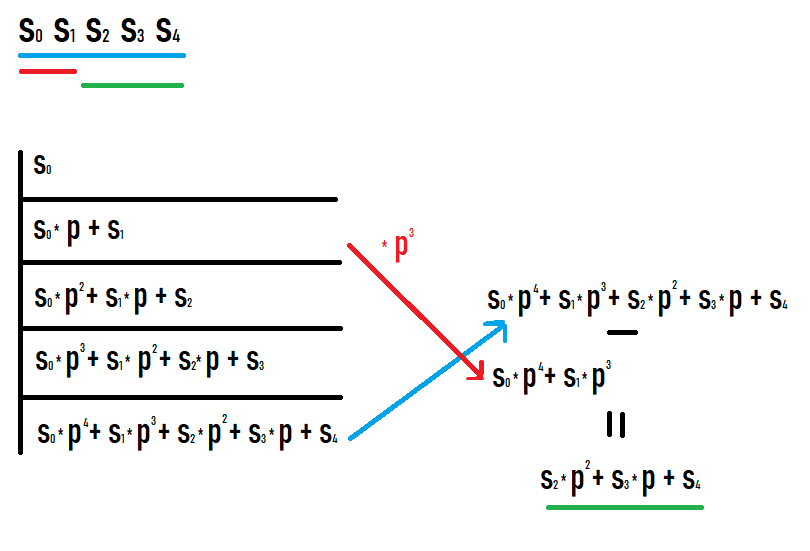
このようなアクションの結果として、元のシーケンスのサブセグメントのハッシュが得られます。さらに、このハッシュは、このサブセグメントに等しいシーケンスからのハッシュとみなした場合のハッシュと等しくなります (他の値と比較するために次数などの追加の変換は必要ありません)。
ここで明確にしておくべき点は次の 2 つです
。
1) r-l+1 乗の p を素早く乗算するには、p modulo mod のすべての可能なべき乗を事前に計算する必要があります。
2) すべての計算はモジュロモジュロで実行されるため、プレフィックス ハッシュを減算すると負の数が得られる可能性があることに注意してください。これを回避するには、減算する前に常に mod を追加します。また、乗算とすべての加算の後に剰余値を取得することを忘れないでください。
コードでは次のようになります。
#include <bits/stdc++.h>
名前空間 std を使用します。
typedef 長い長いll;
const int MAXN = 1000003;
// ベースモジュールとハッシュモジュール
ll p、mod;
// プレフィックスハッシュと指数 p
h[MAXN]、pows[MAXN];
// サブセグメント [l;r] のハッシュを計算します
ll get_segment_hash(int l, int r) {
return (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod;
}
int main()
{
// どうにかして p と mod を取得します
// 累乗 p を事前計算します
pows[0] = 1;
for (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
///
// 主な問題の解決策
///
0 を返します。
}