시퀀스의 해시를 계산하는 대신 각 접두사에 값을 저장할 수 있습니다. 해당 접두사와 동일한 시퀀스의 해시 값이 됩니다.
이러한 구조를 사용하면 이 시퀀스의 하위 세그먼트에 대한 해시 값을 빠르게 계산할 수 있습니다(접두사 합계와 유사).
하위 세그먼트 [l;r]의 해시를 계산하려면 접두사 r에 대한 해시를 가져와 r-l+1의 거듭제곱에 p를 곱한 접두사 l-1에 대한 해시를 빼야 합니다. 접두사에 값을 쓰고 무슨 일이 일어나는지 보면 이것이 왜 그렇게 분명해집니다. 이 사진을 보고 성공하시길 바랍니다.
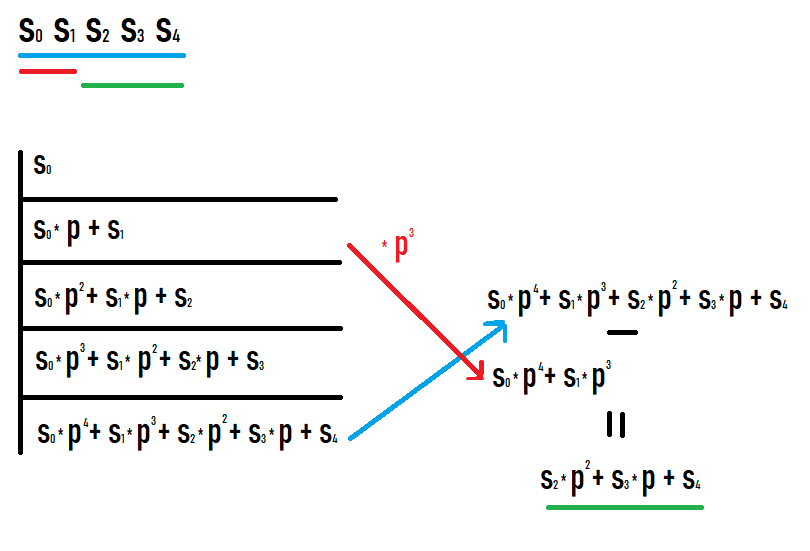
이러한 작업의 결과로 원래 시퀀스의 하위 세그먼트에 대한 해시를 얻습니다. 또한 이 해시는 이 하위 세그먼트와 동일한 시퀀스의 해시로 간주되는 경우의 해시와 동일합니다(다른 값과 비교하기 위해 각도 등의 추가 변환이 필요하지 않음).
여기서 명확히 해야 할 두 가지 사항이 있습니다.
1) p에 r-l+1의 거듭제곱을 빠르게 곱하려면 p modulo mod의 가능한 모든 거듭제곱을 미리 계산해야 합니다.
2) 우리는 모든 계산을 modulo modulo로 수행하므로 접두사 해시를 뺀 후 음수를 얻을 수 있음을 기억해야 합니다. 이를 방지하기 위해 빼기 전에 항상 mod를 추가할 수 있습니다. 또한 곱셈과 모든 덧셈 후에 모듈로 값을 취하는 것을 잊지 마십시오.
코드에서는 다음과 같습니다.
#include <bits/stdc++.h>
네임스페이스 표준 사용;
typedef 긴 longll;
const int MAXN = 1000003;
// 기본 및 해시 모듈
llp, 모드;
// 접두어 해시와 지수 p
h[MAXN], pows[MAXN];
// 하위 세그먼트 [l;r]의 해시 계산
ll get_segment_hash(int l, int r) {
return (h[r] + mod - h[l - 1] * pows[r - l + 1] % 모드) % 모드;
}
정수 메인()
{
// 어떻게든 p와 mod를 얻습니다.
// 거듭제곱 p를 미리 계산
pows[0] = 1;
for (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
//
// 주요 문제 해결
//
0을 반환합니다.
}