Prosedur atau fungsi mungkin mengandungi panggilan ke prosedur lain di dalamnya. Termasuk, subrutin boleh memanggil dirinya sendiri. Dalam kes ini, komputer tidak peduli. Dia juga, seperti biasa, secara konsisten melaksanakan perintah yang dia temui dari atas ke bawah.
Jika anda ingat matematik, maka di sana anda boleh bertemu prinsip aruhan matematik. Ia adalah seperti berikut:
beberapa pernyataan adalah benar untuk setiap n semula jadi jika
1. ia sah untuk n = 1 dan
2. daripada kesahihan pernyataan untuk sebarang n = k semula jadi sewenang-wenangnya ia mengikuti bahawa ia adalah benar untuk n = k+1.
Dalam pengaturcaraan, teknik ini dipanggil rekursi
Rekursi ialah cara untuk mentakrifkan set objek dari segi set itu sendiri, berdasarkan kes asas mudah yang diberikan.
Rekursif juga akan dipanggil prosedur (fungsi) yang memanggil dirinya secara langsung atau melalui prosedur dan fungsi lain
Contoh prosedur rekursif:
void Rec(int a)
{
jika (a>0) Rec(a-1);
cout << a;
}
Secara skematik, kerja rekursi boleh diwakili oleh carta alir
Prosedur Rec() dilaksanakan dengan parameter 3. Kemudian, di dalam prosedur dengan parameter 3, prosedur dengan parameter 2 dipanggil, dan seterusnya, sehingga prosedur dengan parameter 0 dipanggil. Apabila prosedur dengan parameter 0 dipanggil, panggilan rekursif sudah tidak akan berlaku dan prosedur dengan parameter 0 akan mencetak nombor 0 dan ditamatkan. Kemudian kawalan dipindahkan kembali ke prosedur dengan parameter 1, ia juga menyelesaikan kerjanya dengan mencetak nombor 1, dan seterusnya. sebelum prosedur dengan parameter 3.
Semua prosedur yang dipanggil disimpan dalam ingatan sehingga mereka menyelesaikan kerja mereka. Bilangan prosedur serentak dipanggil kedalaman rekursi.
|
Rekursi. Simulasi Gelung
Kami telah melihat bahawa rekursi ialah pelaksanaan berulang arahan yang terkandung dalam subrutin. Dan ini, pada gilirannya, adalah serupa dengan kerja kitaran. Terdapat bahasa pengaturcaraan di mana binaan gelung tidak hadir sama sekali, contohnya, Prolog.
Mari cuba meniru kerja gelung untuk.
Gelung for mengandungi pembolehubah pembilang langkah. Dalam subrutin rekursif, pembolehubah sedemikian boleh diluluskan sebagai parameter.
// Prosedur LoopImitation() dengan dua parameter.
// Parameter pertama – pembilang langkah, parameter kedua – jumlah bilangan langkah.
batal LoopImitation(int i, int n)
{
cout << "Hello N" << i << endl; // Operator akan diulang untuk sebarang nilai i
jika (i < n) // Sehingga pembilang gelung sama dengan n,
{ // panggil contoh baharu prosedur, dengan parameter i+1 (pergi ke nilai seterusnya i).
LoopImitation(i + 1, n);
}
}
|
Rekursi dan lelaran
Untuk memahami rekursi, anda perlu memahami rekursi...
Lelaran dalam pengaturcaraan - satu langkahproses pemprosesan data kitaran.
Selalunya algoritma berulang pada langkah semasa (lelaran) menggunakan hasil operasi atau tindakan yang sama yang dikira pada langkah sebelumnya. Satu contoh pengiraan sedemikian ialah pengiraan perhubungan berulang.
Contoh mudah nilai rekursif ialah faktorial: \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\).
Pengiraan nilai pada setiap langkah (lelaran) ialah \(N=N \cdot i\) . Apabila mengira nilai \(N\), kami mengambil nilai yang telah disimpan \(N\).< br />
Faktorial nombor juga boleh diterangkan menggunakan formula berulang:
\(\begin{equation*} n!= \begin{cases} 1 &\text{n <= 1,}\\ (n-1)! \cdot n &\text{n > 1.} \end{cases} \end{equation*}\)
Anda mungkin perasan bahawa penerangan ini tidak lebih daripada fungsi rekursif.
Di sini baris pertama (\(n <= 1\)) ialah huruf asas (syarat penamatan rekursi) dan baris kedua ialah peralihan ke langkah seterusnya. < br />
| Fungsi faktorial rekursif |
Algoritma lelaran |
|
int Faktorial(int n)
{
jika (n > 1)
kembali n * Faktorial(n - 1);
lain kembali 1;
}
|
x = 1;
untuk (i = 2; i <= n; i++)
x = x * i;
cout << x;
|
Perlu difahami bahawa panggilan fungsi melibatkan beberapa overhed tambahan, jadi pengiraan faktorial bukan rekursif akan menjadi lebih pantas sedikit.
Kesimpulan:di mana anda boleh menulis program dengan algoritma berulang yang mudah, tanpa rekursi, maka anda perlu menulis tanpa rekursi. Namun begitu, terdapat kelas masalah yang besar di mana proses pengiraan dilaksanakan hanya dengan rekursi.
Sebaliknya, algoritma rekursif selalunya lebih mudah difahami.
Tugas
Dalam abjad bahasa suku "Tumba-Yumba"; empat huruf: "K", "L", "M" dan "N". Anda perlu memaparkan semua perkataan yang terdiri daripada n huruf yang boleh dibina daripada huruf abjad ini.
Masalahnya ialah masalah kekerasan biasa yang boleh dikurangkan kepada masalah yang lebih kecil.
Kami akan menggantikan huruf secara berurutan untuk perkataan itu.
Kedudukan pertama perkataan boleh menjadi salah satu daripada 4 huruf abjad (K. L, M, N).
Mari kita letakkan huruf K dahulu. Kemudian, untuk mendapatkan semua varian dengan huruf pertama K, anda perlu menghitung semua kemungkinan gabungan huruf dalam baki n - 1 kedudukan dan seterusnya. (lihat gambar).
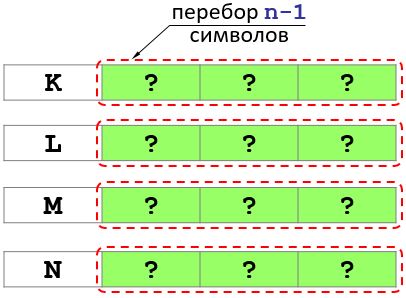 Oleh itu, masalah dikurangkan kepada menyelesaikan empat masalah panjang n - 1.
Lelaran ke atas n aksara secara rekursif
w[0]='K'; // lelaran ke atas aksara L-1 yang terakhir
w[0]='L'; // lelaran ke atas aksara L-1 yang terakhir
w[0]='M'; // lelaran ke atas aksara L-1 yang terakhir
w[0]='N'; // lelaran ke atas aksara L-1 yang terakhir
w - rentetan aksara yang menyimpan perkataan yang berfungsi.
Oleh itu, kami mendapat rekursi. Kami boleh mengatur penyelesaian masalah dalam bentuk prosedur rekursif.
Ia kekal untuk menentukan bila rekursi akan berakhir? Apabila semua aksara ditetapkan, iaitu bilangan aksara yang ditetapkan ialah n. Dalam kes ini, anda perlu memaparkan perkataan yang terhasil pada skrin dan keluar dari prosedur.
Program C++ akan kelihatan seperti ini.
#include<iostream>
menggunakan ruang nama std;
batal TumbaWords( rentetan A, rentetan &w, int N )
// w - parameter boleh ubah (hasil rentetan)
// Prosedur TumbaWords diluluskan abjad sebagai rentetan aksara,
// perkataan perkataan dan bilangan aksara yang telah ditetapkan (sebelumnya – 0).
{
int i;
jika (N == w.size())
{
// jika semua aksara telah ditetapkan kepada perkataan,
// maka perlu mengeluarkan rentetan dan menamatkan prosedur
cout << w<< endl;
kembali;
}
untuk ( i = 1; i < A.size(); i ++ )
{
// jika syarat di atas adalah palsu (iaitu, tidak semua aksara dijarakkan,
// kemudian dalam gelung kita pergi melalui semua aksara abjad dan
// letakkan aksara secara bergantian pada ruang kosong pertama
w[N] = A[i];
TumbaWords ( A, w, N+1 );
}
}
utama()
{
intn;
kata rentetan;
intn;
cin>> n;
word.resize(n); // tambah rentetan kepada saiz n
TumbaWords( "KLMN", perkataan, 0 );
}
PERHATIKAN bahawa w ialah parameter boleh ubah (rentetan hasil)!
|
|