|
|
Daripada hanya mengira cincang jujukan, kita boleh menyimpan nilai pada setiap awalannya. Ambil perhatian bahawa ini akan menjadi nilai cincang untuk jujukan yang sama dengan awalan yang sepadan.
Dengan struktur sedemikian, anda boleh mengira nilai cincang dengan cepat untuk mana-mana subsegmen jujukan ini (serupa dengan jumlah awalan).
Jika kita ingin mengira cincang subsegmen [l;r], maka kita perlu mengambil cincang pada awalan r dan tolak cincang pada awalan l-1 didarab dengan p kepada kuasa r-l+1. Mengapa ini menjadi jelas jika anda menulis nilai pada awalan dan melihat apa yang berlaku. Saya harap anda berjaya melihat gambar ini.
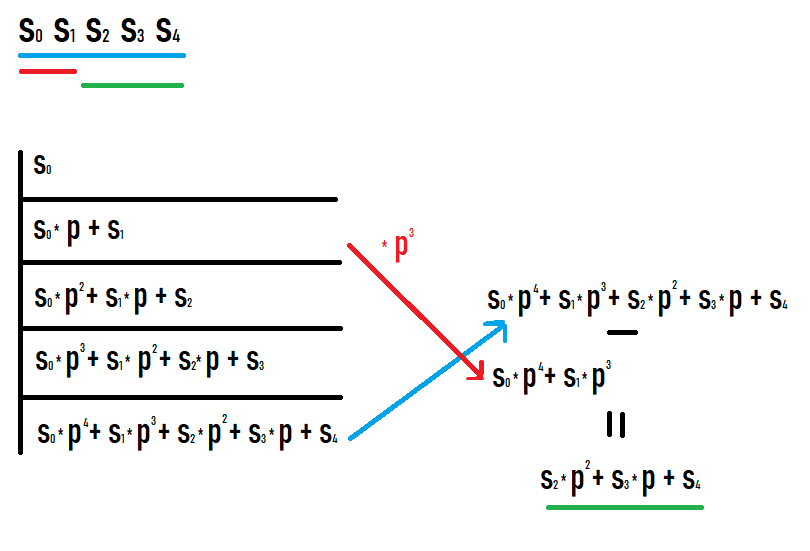
Hasil daripada tindakan sedemikian, kami mendapat cincang subsegmen daripada jujukan asal. Selain itu, cincang ini adalah sama dengan cincangan jika ia dianggap sebagai cincang daripada jujukan yang sama dengan subsegmen ini (tiada penukaran tambahan darjah atau seumpamanya diperlukan untuk dibandingkan dengan nilai lain).
Terdapat dua perkara yang perlu dijelaskan di sini:
1) Untuk mendarab dengan cepat dengan p kepada kuasa r-l+1, adalah perlu untuk mengira awal semua kuasa yang mungkin bagi mod modulo p.
2) Perlu diingat bahawa kami melakukan semua pengiraan modulo modulo, dan oleh itu mungkin ternyata selepas menolak cincang awalan, kami akan mendapat nombor negatif. Untuk mengelakkan ini, anda sentiasa boleh menambah mod sebelum menolak. Juga, jangan lupa untuk mengambil nilai modulo selepas pendaraban dan semua penambahan.
Dalam kod ia kelihatan seperti ini:
#include <bits/stdc++.h>
menggunakan ruang nama std;
typedef long longll;
const int MAXN = 1000003;
// modul asas dan cincang
ll p, mod;
// awalan cincang dan eksponen p
h[MAXN], pows[MAXN];
// mengira cincangan subsegmen [l;r]
ll get_segment_hash(int l, int r) {
pulangan (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod;
}
int utama()
{
// entah bagaimana dapatkan p dan mod
// prakira kuasa p
pows[0] = 1;
untuk (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
//
// penyelesaian masalah utama
//
pulangan 0;
}
|
Jika kita mempunyai cincang rentetan A bersamaan dengan hA dan cincang rentetan B sama dengan hB, maka kami boleh mengira cincang rentetan AB dengan cepat:
hAB = hA * p|B| + hB <- mengira semua modulo
di mana |B| - panjang tali B.
|
Selain jujukan, anda juga boleh set cincang. Iaitu, set objek tanpa susunan padanya. Ia dikira mengikut formula berikut:
hash(A) = \(\sum_{a \in A} p^{ord(a)}\) <- mengira semua modulo
di mana ord ialah fungsi yang menetapkan kepada objek bagi set nombor ordinal mutlaknya di antara semua objek yang mungkin (contohnya, jika objek adalah nombor asli, maka ord(x) = x, dan jika huruf Latin huruf kecil, maka ord(& #39;a' ;) = 1, ord('b') = 2 dsb.)
Iaitu, untuk setiap objek kita mengaitkan nilai yang sama dengan asas dengan kuasa nombor objek ini dan merumuskan semua nilai ini untuk mendapatkan cincangan keseluruhan set. Seperti yang jelas daripada formula, cincang mudah dikira semula jika elemen ditambah atau dialih keluar daripada set (hanya tambah atau tolak nilai yang diperlukan). Logik yang sama, jika tidak satu elemen ditambah atau dialih keluar, tetapi set lain (hanya tambah / tolak cincangnya).
Seperti yang anda sudah faham, elemen tunggal dianggap sebagai set saiz 1, yang mana kita boleh mengira cincangan. Dan set yang lebih besar hanyalah gabungan set tunggal tersebut, di mana dengan menggabungkan set, kami menambah cincangnya.
Sebenarnya, ini masih cincang polinomial yang sama, tetapi sebelum pekali pada pm , kami mempunyai nilai daripada unsur jujukan di bawah nombor n - m - 1 (dengan n ialah panjang jujukan), dan kini ini ialah bilangan unsur dalam set yang nombor ordinal mutlaknya adalah sama dengan m.
Dalam pencincangan sedemikian, seseorang mesti mengambil tapak yang cukup besar (lebih besar daripada saiz set maksimum), atau menggunakan pencincangan berganda untuk mengelakkan situasi di mana set objek p dengan nombor ordinal mutlak m mempunyai cincangan yang sama seperti set dengan satu objek dengan mutlak nombor ordinal m+1.
|
Terdapat juga beberapa cara untuk mencincang pokok berakar dengan cekap.
Salah satu kaedah ini disusun seperti berikut:
Kami memproses bucu secara rekursif, mengikut urutan traversal secara mendalam. Kami akan menganggap bahawa cincangan satu bucu adalah sama dengan p. Untuk bucu dengan kanak-kanak, kami mula-mula menjalankan algoritma untuk mereka, kemudian melalui kanak-kanak kami akan mengira cincang subpokok semasa. Untuk melakukan ini, pertimbangkan cincangan subpokok kanak-kanak sebagai jujukan nombor dan kirakan cincang daripada jujukan ini. Ini akan menjadi cincang subpokok semasa.
Jika susunan pada kanak-kanak itu tidak penting bagi kami, maka sebelum mengira cincang, kami mengisih jujukan cincang daripada subpokok kanak-kanak dan kemudian mengira cincang daripada jujukan yang diisih.
Dengan cara ini anda boleh menyemak isomorfisme pokok - hanya mengira cincang tanpa susunan pada kanak-kanak (iaitu, setiap kali mengisih cincang kanak-kanak). Dan jika cincangan akar sepadan, maka pokok itu adalah isomorfik, jika tidak, tidak.
Untuk pokok yang tidak berakar, semuanya berlaku dengan cara yang sama, tetapi centroid mesti diambil sebagai akar. Atau pertimbangkan sepasang cincang jika terdapat dua centroid.
|