Problem
Asya ama muito os animais. Ela recentemente comprou n gatinhos, deu a eles identificadores numéricos de 1 a n e os colocou em um cercado. O aviário é uma fileira de n células, também numeradas de 1 a n. As células vizinhas são separadas por partições de malha, no total existem n & menos; 1 partições no gabinete. Inicialmente, exatamente um gatinho com algum número se estabeleceu em cada célula.
Observando os gatinhos, Asya percebeu que eles são muito amigáveis e alguns pares de gatinhos que vivem em celas vizinhas querem muito brincar um com o outro. Para não privá-los desse prazer, Asya começou a remover as divisórias entre as células adjacentes, tornando-as maiores.
No i-ésimo dia, Asya fez o seguinte.
Percebi que alguns gatinhos x
i e y
i, vivendo em celas vizinhas no i-ésimo dia, querem brincar.
Retirei a divisória entre essas celas, transformando-as em uma só, onde foram parar todos os gatinhos das duas celas anteriores.
Como Asya não devolveu as partições, após n & menos; 1 dia o recinto tornou-se uma única cela na qual viviam todos os gatinhos. Sendo muito pedante, Asya anotou os IDs dos gatinhos x
i e y
i para cada um dos n&menos;1 dias em um diário especial.
Você conseguiu uma revista com essas informações, mas não sabe como os gatinhos foram acomodados nas celas em primeiro lugar. Encontre qualquer distribuição de gatinhos em n células originais que não contradiga os dados do log.
Entrada
A primeira linha contém um inteiro n (
\(2 \leq n \leq 150000\)) — número de gatinhos.
As próximas n&menos;1 linhas contêm pares de números inteiros x
i , y
i (
\(1 \leq x_i , y_i, \leq n,x_i \neq y_i\) ) — identificadores de gatinhos, entre as células das quais a partição foi removida no dia i. É garantido que os gatinhos xi e yi não estão na mesma célula como resultado da fusão de células anterior.
Impressão
Imprima n inteiros distintos p
i (
\(1 \leq p_i \leq n\)), onde p
i — o identificador do gatinho que originalmente morava na cela de número i. Se houver várias respostas possíveis, imprima qualquer uma delas.
Observação
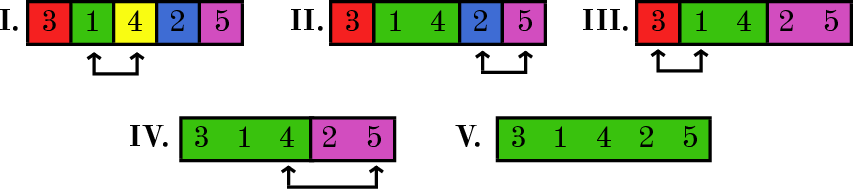
Na resposta, por exemplo, é dado um dos possíveis assentamentos iniciais dos gatinhos, existem outras respostas. A imagem abaixo mostra como as células foram mescladas para esta colocação inicial de gatinhos. Observe que, com esse arranjo, os gatinhos que se tornaram amigos a cada dia, de acordo com o diário de Asya, estão em celas adjacentes.
| Entrada |
Saída |
5
14
25
3 1
4 5 |
3 1 4 2 5 |