Um procedimento ou função pode conter uma chamada para outro procedimento dentro dele. Inclusive, a sub-rotina pode chamar a si mesma. Nesse caso, o computador não se importa. Ele também, como sempre, executa consistentemente os comandos que conhece de cima para baixo.
Se você se lembra da matemática, pode encontrar o princípio da indução matemática. É o seguinte:
alguma afirmação é verdadeira para todo natural n se
1. é válido para n = 1 e
2. da validade da afirmação para qualquer natural arbitrário n = k segue-se que é verdade para n = k+1.
Na programação, essa técnica é chamada de recursão
Recursão é uma forma de definir um conjunto de objetos em termos do próprio conjunto, com base em casos básicos simples fornecidos.
Recursivo também será chamado de procedimento (função) que chama a si mesmo diretamente ou por meio de outros procedimentos e funções
Exemplo de procedimento recursivo:
void Rec(int a)
{
se (a>0) Rec(a-1);
cout << a;
}
Esquematicamente, o trabalho de recursão pode ser representado por um fluxograma
O procedimento Rec() é executado com o parâmetro 3. Em seguida, dentro do procedimento com o parâmetro 3, é chamado o procedimento com o parâmetro 2, e assim sucessivamente, até que seja chamado o procedimento com o parâmetro 0. Quando o procedimento com o parâmetro parâmetro 0 for chamado, a chamada recursiva já não acontecerá e o procedimento com parâmetro 0 imprimirá o número 0 e terminará. Em seguida, o controle é transferido de volta para o procedimento com o parâmetro 1, ele também termina seu trabalho imprimindo o número 1 e assim por diante. antes do procedimento com o parâmetro 3.
Todos os procedimentos chamados são armazenados na memória até que concluam seu trabalho. O número de procedimentos simultâneos é chamado de profundidade de recursão.
|
Recursão. Simulação de Loop
Vimos que a recursão é a execução repetida de instruções contidas em uma sub-rotina. E isso, por sua vez, é semelhante ao trabalho do ciclo. Existem linguagens de programação nas quais a construção do loop está ausente, por exemplo, Prolog.
Vamos tentar simular o funcionamento do loop for.
O loop for contém uma variável de contador de passos. Em uma sub-rotina recursiva, tal variável pode ser passada como um parâmetro.
// Procedimento LoopImitation() com dois parâmetros.
// Primeiro parâmetro – contador de passos, segundo parâmetro – número total de passos.
void LoopImitation(int i, int n)
{
cout << "Olá N" << e << endl; // Operador a ser repetido para qualquer valor de i
if (i < n) // Até que o contador do loop seja igual a n,
{ // chama uma nova instância do procedimento, com o parâmetro i+1 (vai para o próximo valor i).
LoopImitation(i + 1, n);
}
}
|
Recursão e iteração
Para entender a recursão, você precisa entender a recursão...
Iteração na programação - uma etapade um processo cíclico de processamento de dados.
Freqüentemente, algoritmos iterativos na etapa atual (iteração) usam o resultado da mesma operação ou ação calculada nas etapas anteriores. Um exemplo desses cálculos é o cálculo das relações de recorrência.
Um exemplo simples de valor recursivo é o fatorial: \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\).
O cálculo do valor em cada etapa (iteração) é \(N=N \cdot i\) . Ao calcular o valor de \(N\), tomamos o valor já armazenado \(N\).< br />
O fatorial de um número também pode ser descrito usando a fórmula recorrente:
\(\begin{equation*} n!= \begin{cases} 1 &\text{n <= 1,}\\ (n-1)! \cdot n &\text{n > 1.} \end{casos} \end{equação*}\)
Você pode perceber que esta descrição nada mais é do que uma função recursiva.
Aqui, a primeira linha ( \(n <= 1\)) é o caso base (condição de término da recursão) e a segunda linha é a transição para a próxima etapa. < br />
| Função fatorial recursiva |
Algoritmo iterativo |
|
int Fatorial(int n)
{
se (n > 1)
return n * Fatorial(n - 1);
caso contrário, retorne 1;
}
|
x = 1;
para (i = 2; i <= n; i++)
x = x * i;
cout << x;
|
Deve ser entendido que as chamadas de função envolvem alguma sobrecarga adicional, portanto, um cálculo fatorial não recursivo será um pouco mais rápido.
Conclusão: onde você pode escrever um programa com um algoritmo iterativo simples, sem recursão, então você precisa escrever sem recursão. Ainda assim, existe uma grande classe de problemas onde o processo computacional é implementado apenas por recursão.
Por outro lado, algoritmos recursivos costumam ser mais compreensíveis.
|
Tarefa
No alfabeto da língua da tribo "Tumba-Yumba"; quatro letras: "K", "L", "M" e "N". Você precisa exibir todas as palavras que consistem em n letras que podem ser construídas a partir das letras deste alfabeto.
O problema é um problema normal de força bruta que pode ser reduzido a um problema menor.
Substituiremos sequencialmente as letras da palavra.
A primeira posição de uma palavra pode ser uma das 4 letras do alfabeto (K. L, M, N).
Vamos colocar a letra K primeiro. Então, para obter todas as variantes com a primeira letra K, você precisa enumerar todas as combinações possíveis de letras nas posições n - 1 restantes e assim por diante. (veja a foto).
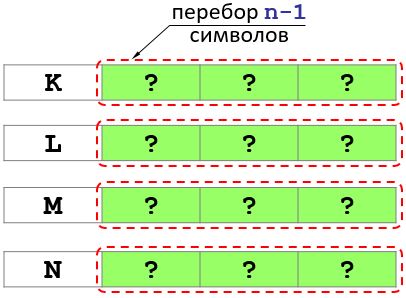 Assim, o problema se reduz a resolver quatro problemas de comprimento n - 1.
Iterar sobre n caracteres recursivamente
w[0]='K'; // itera sobre os últimos caracteres L-1
w[0]='L'; // itera sobre os últimos caracteres L-1
w[0]='M'; // itera sobre os últimos caracteres L-1
w[0]='N'; // itera sobre os últimos caracteres L-1
w - uma cadeia de caracteres que armazena a palavra de trabalho.
Assim, temos recursão. Podemos organizar a solução do problema na forma de um procedimento recursivo.
Resta determinar quando a recursão terminará? Quando todos os caracteres são definidos, ou seja, o número de caracteres definidos é n. Nesse caso, você precisa exibir a palavra resultante na tela e sair do procedimento.
O programa C++ ficará assim.
#include<iostream>
usando namespace std;
void TumbaWords( string A, string &w, int N )
// w - parâmetro alterável (string-result)
// O procedimento TumbaWords recebe o alfabeto como uma string de caracteres,
// a palavra word e o número de caracteres já definidos (precedendo – 0).
{
int eu;
if (N == w.size())
{
// se todos os caracteres já tiverem sido definidos para a palavra,
// então é necessário enviar uma string e terminar o procedimento
cout << w<< endl;
retornar;
}
for ( i = 1; i < A.size(); i++ )
{
// se a condição acima for falsa (ou seja, nem todos os caracteres são espaçados,
// então no loop passamos por todos os caracteres do alfabeto e
// coloca alternadamente o caractere no primeiro espaço livre
w[N] = A[i];
Palavras Tumba ( A, w, N+1 );
}
}
principal()
{
int;
palavra-chave;
int;
cin>> n;
palavra.resize(n); // aumenta a string para o tamanho n
TumbaPalavras("KLMN", palavra, 0);
}
OBSERVE que w é um parâmetro mutável (string de resultado)!
|