|
|
Em vez de apenas calcular o hash de uma sequência, podemos armazenar o valor em cada um de seus prefixos. Observe que esses serão valores de hash para sequências iguais ao prefixo correspondente.
Com essa estrutura, você pode calcular rapidamente o valor de hash para qualquer subsegmento dessa sequência (semelhante às somas de prefixos).
Se quisermos calcular o hash do subsegmento [l;r], precisamos pegar o hash no prefixo r e subtrair o hash no prefixo l-1 multiplicado por p à potência de r-l+1. Por que isso acontece fica claro se você escrever os valores nos prefixos e ver o que acontece. Espero que consiga olhar para esta foto.
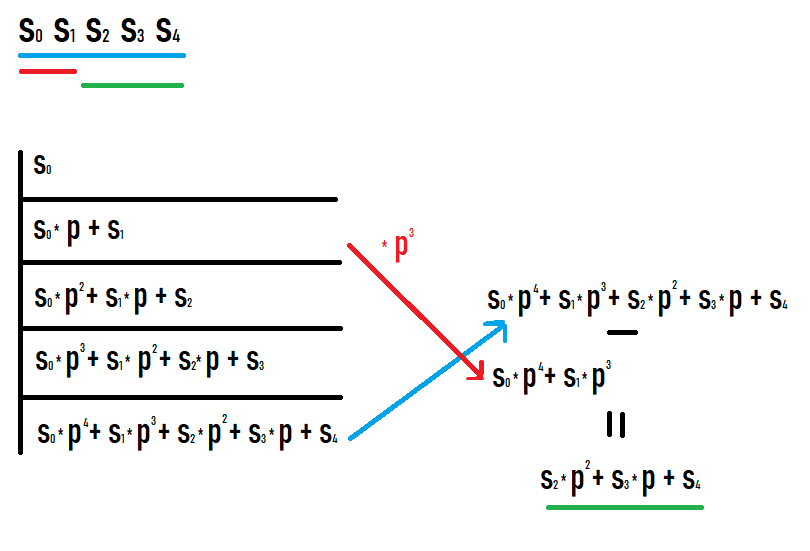
Como resultado de tais ações, obtemos um hash de um subsegmento da sequência original. Além disso, este hash é igual ao que se fosse considerado como um hash de uma sequência igual a este subsegmento (não são necessárias conversões adicionais de graus ou similares para comparar com outros valores).
Há dois pontos a serem esclarecidos aqui:
1) Para multiplicar rapidamente por p à potência r-l+1, é necessário pré-calcular todas as potências possíveis de p módulo mod.
2) Deve-se lembrar que realizamos todos os cálculos módulo módulo e, portanto, pode acontecer que, após subtrair os hashes do prefixo, obteremos um número negativo. Para evitar isso, você sempre pode adicionar mod antes de subtrair. Além disso, não se esqueça de calcular o valor do módulo após as multiplicações e todas as adições.
No código fica assim:
#include <bits/stdc++.h>
usando namespace std;
typedef long longll;
const int MAXN = 1000003;
// módulo base e hash
ll p, mod;
// prefixo hash e expoentes p
h[MAXN], pows[MAXN];
// calculando o hash do subsegmento [l;r]
ll get_segment_hash(int l, int r) {
return (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod;
}
int main()
{
// de alguma forma obter p e mod
// pré-calcula as potências p
poder[0] = 1;
para (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
//
// solução do problema principal
//
retorna 0;
}
|
Se tivermos um hash da string A igual a hA e um hash da string B igual a hB, podemos calcular rapidamente o hash da string AB:
hAB = hA * p|B| + hB <- contando tudo modulo
onde |B| - o comprimento da corda B.
|
Além das sequências, você também pode criar conjuntos de hash. Ou seja, conjuntos de objetos sem ordem neles. É calculado de acordo com a seguinte fórmula:
hash(A) = \(\sum_{a \in A} p^{ord(a)}\) <- contando tudo modulo
onde ord é uma função que atribui a um objeto do conjunto seu número ordinal absoluto entre todos os objetos possíveis (por exemplo, se os objetos são números naturais, então ord(x) = x, e se letras latinas minúsculas, então ord(& #39;a' ;) = 1, ord('b') = 2 etc.)
Ou seja, para cada objeto associamos um valor igual à base à potência do número desse objeto e somamos todos esses valores de forma a obter um hash de todo o conjunto. Como fica claro na fórmula, o hash é facilmente recalculado se um elemento for adicionado ou removido do conjunto (basta adicionar ou subtrair o valor necessário). Mesma lógica, se não forem adicionados ou removidos elementos únicos, mas outros conjuntos (basta adicionar/subtrair seu hash).
Como você já pode entender, os elementos individuais são considerados como conjuntos de tamanho 1, para os quais podemos calcular o hash. E conjuntos maiores são simplesmente uma união de tais conjuntos únicos, onde, combinando conjuntos, adicionamos seus hashes.
Na verdade, este ainda é o mesmo hash polinomial, mas antes do coeficiente em pm , tínhamos o valor do elemento de sequência sob o número n - m - 1 (onde n é o comprimento da sequência), e agora este é o número de elementos no conjunto cujo número ordinal absoluto é igual a m.
Em tal hash, deve-se tomar uma base suficientemente grande (maior que o tamanho máximo do conjunto) ou usar hashing duplo para evitar situações em que um conjunto de objetos p com número ordinal absoluto m tem o mesmo hash que um conjunto com um objeto com absoluto número ordinal m+1.
|
Existem também várias maneiras de fazer hash de árvores enraizadas com eficiência.
Um desses métodos é organizado da seguinte forma:
Processamos os vértices recursivamente, em ordem de travessia em profundidade. Assumiremos que o hash de um único vértice é igual a p. Para vértices com filhos, primeiro executamos o algoritmo para eles e, a partir dos filhos, calculamos o hash da subárvore atual. Para fazer isso, considere os hashes das subárvores dos filhos como uma sequência de números e calcule o hash a partir dessa sequência. Este será o hash da subárvore atual.
Se a ordem dos filhos não for importante para nós, antes de calcular o hash, classificamos a sequência de hashes das subárvores filhas e, em seguida, calculamos o hash da sequência classificada.
Dessa forma, você pode verificar o isomorfismo das árvores - basta contar o hash sem ordem nos filhos (ou seja, cada vez classificando os hashes dos filhos). E se os hashes das raízes coincidirem, então as árvores são isomórficas, caso contrário não.
Para árvores não enraizadas, tudo acontece de maneira semelhante, mas o centróide deve ser considerado a raiz. Ou considere um par de hashes se houver dois centróides.
|