Yinelemeyi anlamak için yinelemeyi anlamanız gerekir...
Yineleme programlamada — geniş anlamda — eylemlerin kendilerine çağrılara yol açmadan birçok kez tekrarlandığı veri işleme organizasyonu (%BA%D1%83%D1%80%D1%81%D0%B8%D1%8F'den farklı olarak) title="Tekrarlama" >Yinelemeler). Dar anlamda — tek adımlı döngüsel veri işleme süreci.
Genellikle geçerli adımdaki (yineleme) yinelemeli algoritmalar, önceki adımlarda hesaplanan aynı işlemin veya eylemin sonucunu kullanır. Bu tür hesaplamalara bir örnek, yineleme ilişkilerinin hesaplanmasıdır.
Özyinelemeli değerin basit bir örneği faktöriyeldir:
\(N!=1 \cdot 2 \cdot 3 \cdot \ ... \\cdot N\)
Her adımda (yineleme) değerin hesaplanması şu şekildedir:
\(N=N \cdot i\) .
\(N\) değerini hesaplarken, önceden depolanmış değeri
\(N\) alırız >.
Bir sayının faktöriyeli
yinelenen formül kullanılarak da açıklanabilir:

Bu açıklamanın özyinelemeli bir işlevden başka bir şey olmadığını fark edebilirsiniz.
İşte ilk satır (
\(n <= 1\)) — bu temel durumdur (yinelemenin bitiş koşulu) ve ikinci satır bir sonraki adıma geçiştir.
| Özyinelemeli faktöriyel işlevi şuna benzer |
Faktöriyeli bulmak için algoritmayı olağan, yinelemesiz şekilde karşılaştırın |
işlev Faktöriyel(n: tamsayı): tamsayı;
başla
eğer n > 1 o zaman
Faktöriyel := n * Faktöriyel(n - 1)
başka
Faktöriyel := 1;
bitiş; |
x := 1;
for i := 2 to n do
x := x * ben;
writeln(x); |
İşlev çağrılarının bazı ek yük içerdiği anlaşılmalıdır, bu nedenle özyinelemeli olmayan bir faktöriyel hesaplaması biraz daha hızlı olacaktır.
Sonuç: Basit bir yinelemeli algoritmaya sahip, yinelemesiz bir program yazabileceğiniz yerde, yinelemesiz yazmanız gerekir. Ancak yine de, hesaplama sürecinin yalnızca özyineleme ile uygulandığı geniş bir problem sınıfı vardır.
Öte yandan, özyinelemeli algoritmalar genellikle daha anlaşılırdır.
Problem
Belirli bir doğal sayıdaki basamak sayısını döndüren bir işlev K(n) tanımlayın n:
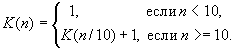
Bir n doğal sayısındaki basamak sayısını hesaplayan özyinelemeli bir fonksiyon yazın.
Запрещенные операторы: for;while;until