n elementin k ile kombinasyonları, her bağlantıda k element toplayan n elementten oluşturulabilen bileşiklerdir; bağlantılar birbirinden yalnızca elemanların kendisinde farklılık gösterirken (düzenlenme sıralarındaki fark dikkate alınmaz).
Örneğin, her biri 2 olan 3 öğeden (a,b,c)(a,b,c) aşağıdaki kombinasyonlar oluşturulabilir: ab,ac,bc.
k ile n öğeden oluşturulabilen tüm olası kombinasyonların sayısı,
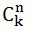
ve şu formülle hesaplanır:
Kombinasyon sayısını bulmanın iki yolu vardır
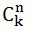
1. n!, k!, (n – k)! ve yukarıdaki formüle göre miktarı hesaplıyoruz, ancak – olası taşma nedeniyle, bu yöntem n <= 12.
ile kullanılabilir.
2. Dinamik programlama ile.
DP, birler üstte ve kenarlarda olacak şekilde Pascal üçgeni gibi görünecek ve her sayı, üstündeki iki sayının toplamına eşittir.
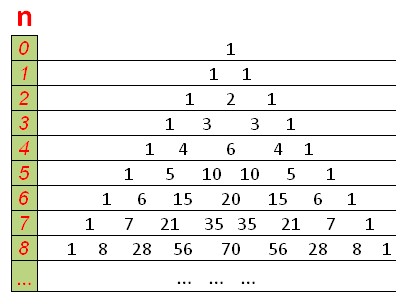
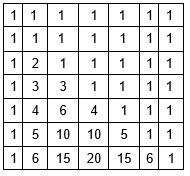
O(n ^2 ) içinde dinamik programlama kullanan kombinasyon sayısını sayan bir işlev:
int C(int n, int k)
{
vektör<vektör<int> > dp(n + 1, vektör<int>(n + 1, 1)); // (n + 1, n + 1) boyutunda bir dp dizisi oluşturun
için (int i = 0; i <= n; i++) // Dizinin i. satırını doldurun
{
için (int j = 1; j < i; j++)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; //(i;j) konumu (i - 1; j - 1) ve (i - 1; j) aracılığıyla yeniden hesaplanıyor
}
}
geri dön dp[n][k]; //dönüş değeri
}