Module: Dijkstra's algorithm


Problem

1/14

Dijkstra: The Beginning (C++)

Theory Click to read/hide

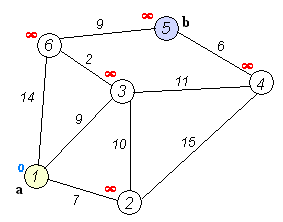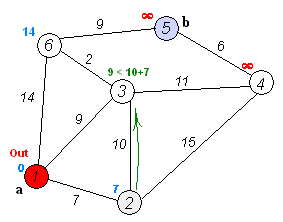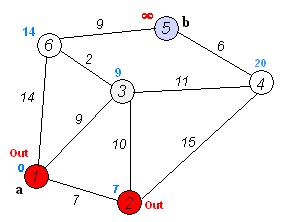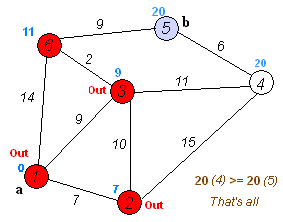
Given a directed or undirected weighted graph with n vertices and m edges. The weights of all edges are non-negative. Some starting vertex s is specified. You need to find the lengths of the shortest paths from vertex s to all other vertices, and also provide a way to print the shortest paths themselves.
 
This problem is called the "single source shortest path problem" (single-source shortest paths problem).

Performs the same tasks as 1-K BFS, but without regard to K. Also, like 1-K BFS, it does not properly handle negative edges

Algorithm:
Dijkstra's algorithm itself consists of N iterations. At the next iteration, the vertex V  with the smallest distance to it from among the vertices not yet marked, this vertex becomes marked and relaxations of neighboring vertices occur from it.


 final asymptotic behavior of the algorithm is: O(n2+ m)

Problem

You are given a directed weighted graph. Find the shortest distance from one given vertex to another.
 
Input
The first line contains three numbers: N, S and F (1≤ N≤ 100, 1≤ S, F≤ N), where N – number of graph vertices, S – initial vertex, and F – final. In the next N lines, enter N numbers each, not exceeding 100, – weight adjacency matrix of the graph, where -1 means no edge between vertices, and any non-negative number – the presence of an edge of given weight. Zeros are written on the main diagonal of the matrix.
 
Output
It is required to display the desired distance or -1 if there is no path between the specified vertices.

Examples
# Input Output
1
3 2 1
0 1 1
4 0 1
2 1 0
 3

time 1000 ms
memory 32 Mb
Rules for program design and list of errors in automatic problem checking

Teacher commentary

Insert the missing code snippets
C++
Write the program below 
#include<iostream>
 
using namespace std;
 
int main()
{
    const int N1 = 110;
    int N, S, F, g[N1][N1], i, j, mini, d[N1];
    bool used[N1];
   
    cin >> N >> S >> F;
   
    fill(used, used + N, false);
   
    fill(d, d + N, 10000000);
   
    for (i = 0; i < N; i++)
    {
        for (j = 0; j < N; j++)
            cin >> g[i][j];
    }
   
    d[S - 1] = 0;
   
    for (i = 0; i < N; i++)
    {
        mini = -1;
       
        for (j = 0; j < N; j++)
        {
            if (!used[j] && (mini == -1 || d[j] < d[mini]))
                mini = j;
        }
       
        used[mini] = true;
       

        
    if (d[F - 1] == 10000000)
        cout << "-1";
    else
        cout << d[F - 1];
}

     

Program check result

To check the solution of the problem, you need to register or log in!