Problem
Asya loves animals very much. She recently purchased n kittens, gave them numeric identifiers from 1 to n, and placed them in an enclosure. The aviary is a row of n cells, also numbered from 1 to n. Neighboring cells are separated by mesh partitions, in total there are n & minus; 1 partitions in the enclosure. Initially, exactly one kitten with some number settled in each cell.
Watching the kittens, Asya noticed that they are very friendly and some pairs of kittens living in neighboring cells really want to play with each other. In order not to deprive them of this pleasure, Asya began to remove the partitions between adjacent cells, making them larger.
On the i-th day, Asya did the following.
I noticed that some kittens x
i and y
i, living in neighboring cells on the i-th day, want to play.
I removed the partition between these cells, turning them into one, in which all the kittens from the two previous cells ended up.
Since Asya did not return the partitions, after n & minus; 1 day the enclosure became a single cell in which all the kittens lived. Being very pedantic, Asya wrote down the kitten IDs x
i and y
i for each of n−1 days in a special journal.
You got a magazine with this information, but you do not know how the kittens were settled in the cells in the first place. Find any distribution of kittens in n original cells that does not contradict the data in the log.
Input
The first line contains an integer n (
\(2 \leq n \leq 150000\)) — number of kittens.
The next n−1 lines contain pairs of integers x
i , y
i (
\(1 \leq x_i , y_i, \leq n,x_i \neq y_i\) ) — identifiers of kittens, between the cells of which the partition was removed on day i. It is guaranteed that kittens xi and yi are not in the same cell as a result of previous cell merging.
Imprint
Print n distinct integers p
i (
\(1 \leq p_i \leq n\)), where p
i — the identifier of the kitten that originally lived in cell number i. If there are several possible answers, print any of them.
Note
In the answer, for example, one of the possible initial settlements of kittens is given, there are other answers. The image below shows how cells were merged for this initial placement of kittens. Please note that with this arrangement, the kittens that became friends on each day according to Asya's journal are in adjacent cells.
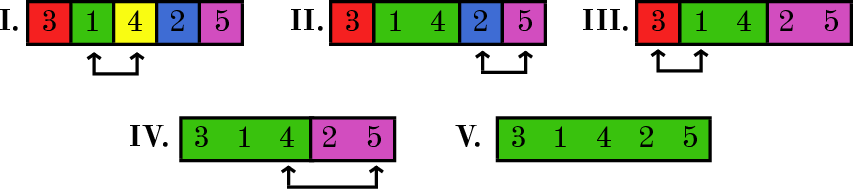
| Input |
Output |
5
14
25
3 1
4 5 |
3 1 4 2 5 |