DFS DFS
Depth first search ( DFS) is one of the main algorithms on graphs. The algorithm runs in O(N + M).
Algorithm
To begin with, we start from the top, consider the children of this top, and if we have never entered them, then we start DFS from them.
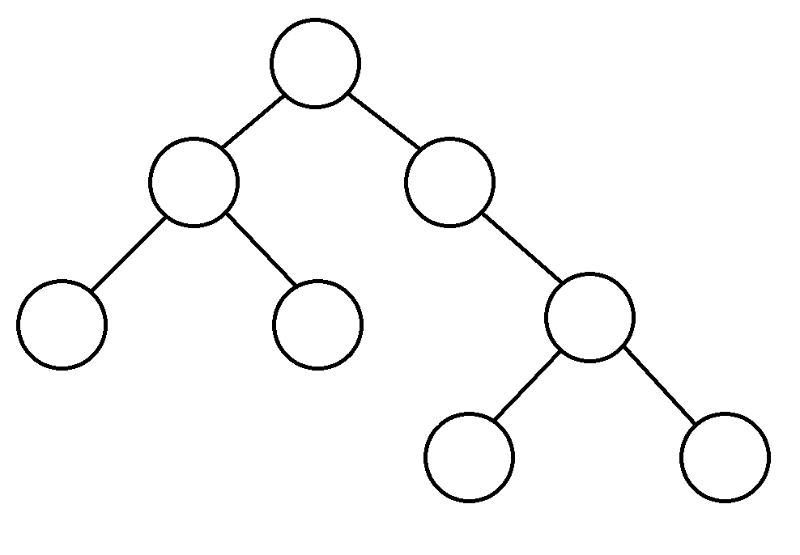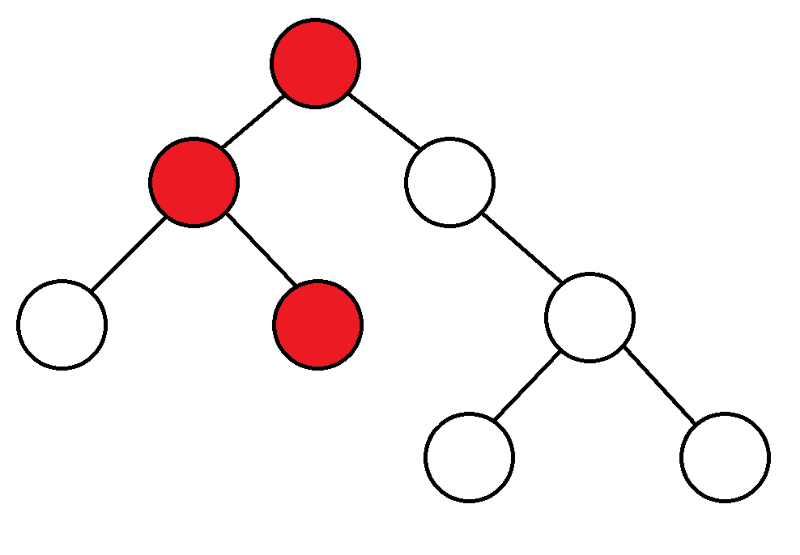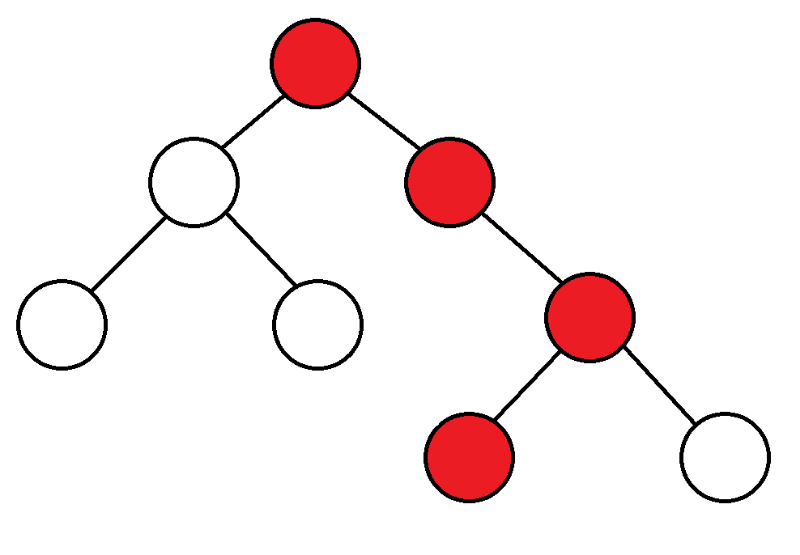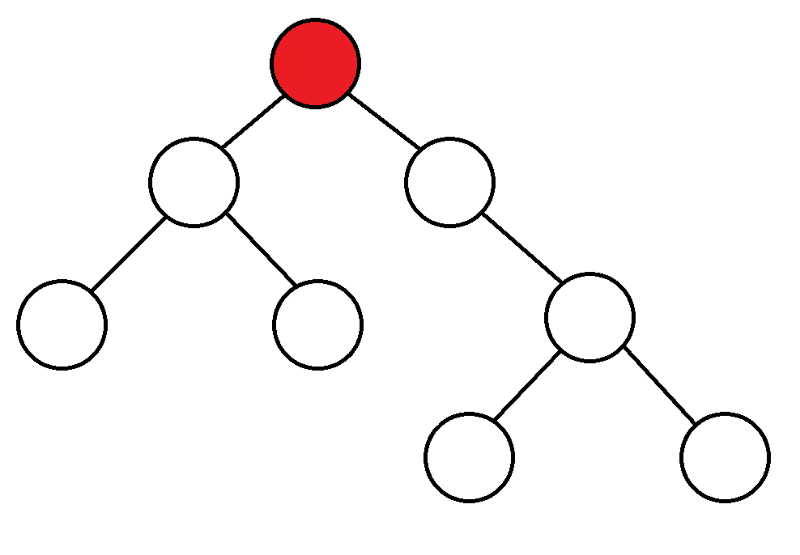
|
DFS DFS
Depth first search ( DFS) is one of the main algorithms on graphs. The algorithm runs in O(N + M).
Algorithm
To begin with, we start from the top, consider the children of this top, and if we have never entered them, then we start DFS from them.

|
Bipartite graph
Bipartite graph - a graph whose vertices can be divided into two sets so that each edge connects the vertices from different sets.
Often in the context of bipartite graphs, the concept of colors vertices is used. Splitting a graph into two parts is called coloring its vertices with two different colors. Each edge must connect vertices of a different color.
DFS.
Algorithm
We start painting from an arbitrary vertex, which we paint in an arbitrary color.
When passing along each edge, paint the next vertex in the opposite color.
If, while iterating over neighboring vertices, we find a vertex that is already painted in the same color as the current one, then there is an odd cycle in the graph, which means that it is not bipartite.
|
The algorithm can be described as follows:
Given a directed graph with n vertices and m edges. It is required to renumber its vertices in such a way that each edge leads from a vertex with a lower number to a vertex with a higher one.
In other words, it is required to find a permutation of vertices (topological order) corresponding to the order given by all the edges of the graph.
We will use depth-first search (dfs(v))
If we add our vertex to the beginning of a list at the time of exit from \(dfs(v)\) , then in the end in this list you get a topological sort.
Thus, the desired topological sort — this is sorted in descending order of exit times.
|