Task
In the alphabet of the language of the tribe "Tumba-Yumba"; four letters: "K", "L", "M" and "N". You need to display all the words consisting of n letters that can be built from the letters of this alphabet.
The problem is a normal brute-force problem that can be reduced to a smaller problem.
We will sequentially substitute letters for the word.
The first position of a word can be one of the 4 letters of the alphabet (K. L, M, N).
Let's put the letter K first. Then, in order to get all variants with the first letter K, you need to enumerate all possible combinations of letters in the remaining n - 1 positions and so on. (see picture).
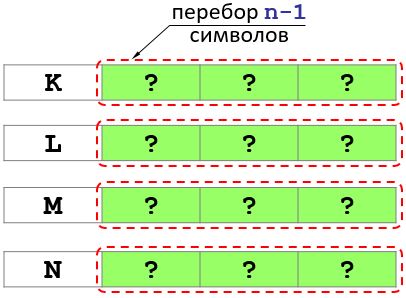 Thus, the problem is reduced to solving four problems of length n - 1.
Iterate over n characters recursively
w[0]='K'; // iterate over the last L-1 characters
w[0]='L'; // iterate over the last L-1 characters
w[0]='M'; // iterate over the last L-1 characters
w[0]='N'; // iterate over the last L-1 characters
w - a character string that stores the working word.
Thus, we got recursion. We can arrange the solution of the problem in the form of a recursive procedure.
It remains to determine when the recursion will end? When all characters are set, that is, the number of set characters is n. In this case, you need to display the resulting word on the screen and exit the procedure.
The C++ program will look like this.
#include<iostream>
using namespace std;
void TumbaWords( string A, string &w, int N )
// w - changeable parameter (string-result)
// The TumbaWords procedure is passed the alphabet as a character string,
// the word word and the number of characters already set (preceding – 0).
{
int i;
if (N == w.size())
{
// if all characters have already been set to the word,
// then it is necessary to output a string and end the procedure
cout << w<< endl;
return;
}
for ( i = 1; i < A.size(); i ++ )
{
// if the condition above is false (that is, not all characters are spaced,
// then in the loop we go through all the characters of the alphabet and
// alternately put the character on the first free space
w[N] = A[i];
TumbaWords ( A, w, N+1 );
}
}
main()
{
intn;
stringword;
intn;
cin>> n;
word.resize(n); // increase string to size n
TumbaWords( "KLMN", word, 0 );
}
NOTE that w is a mutable parameter (result string)!
|