Bar
Bor is a data structure for storing a set of strings, which is a rooted tree with symbols on the edges.
Each boron vertex corresponds to a prefix of some added string. This prefix itself is obtained by sequentially writing characters on the edges on the path from the root to this vertex. At the same time, exactly one vertex corresponds to each existing prefix. Bor root corresponds to an empty string.
Boron example for {be, bee, can, cat, cd}
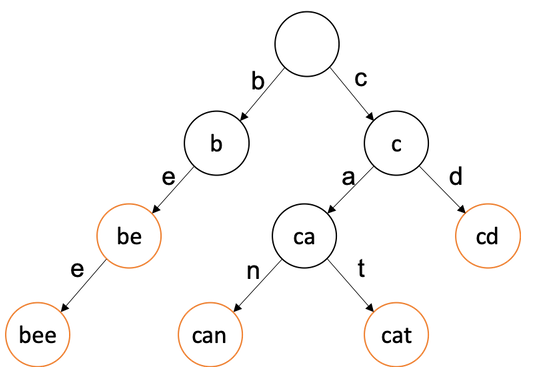
Orange indicates the vertices that correspond to the words from the set themselves. They are called terminals.
Below is the code for storing the boron and adding lines to it. This method stores the bore through an array. There is also an implementation through pointers, which is presented in the code of the task for training.
// alphabet size in considered words
const int alpha = 26;
// structure for the top of the drill
struct Node{
// vector of edges in the form of an adjacency table, that is:
// next[0] - child when jumping over character number 0 ('a')
// next[1] - child when jumping over character number 1 ('b')
// etc.
vectornext;
// Extra options
// in this case, the height of the vertex h and the flag of terminality
int h;
bool term;;
Node(int h) {
next.resize(alph, -1); // initially without edges
this->h = h; // height is equal to specified
term=false; // top is not terminal by default
}
};
// list of vertices, initially root at zero height
vector trie(1, Node(0));
// function for adding a string to the boron
void add(const string& s) {
int v = 0; // number of the current vertex, starting from the root
forn(i, (int)s.size()) {
int c = s[i] - 'a'; // get the number of the current character in the string
// if the desired transition does not yet exist, then we will make a new one
if (trie[v].next[c] == -1) {
trie[v].next[c] = (int)trie.size(); // new vertex number is
// current drill size (with 0-numbering)
trie.push_back(Node(trie[v].h + 1)); // create a new vertex with height 1 more
}
v = trie[v].next[c]; // move along the desired edge
}
// when we got to the top,
// which matches the whole string,
// then mark it as terminal
trie[v].term = true;
}
If you need to support the deletion of rows from the boron, then it will probably turn out to be dishonest. That is, simply remove the terminal flag (or, perhaps, instead of the flag, you will need to store a variable number), and leave the boron tree itself unchanged.
Thus, insertion/search/unfair deletion work in linear time from the length of the query string.
Boron itself, in the worst case, will occupy O(n|Σ|) memory, where n is the total length of all strings, and Σ > - the alphabet of the used strings.
|
To solve this problem, the theory of game analysis will greatly help you: https://e-maxx.ru/algo/games_on_graphs
|