A procedure or function can contain a call to another procedure within it. Including, the subroutine can call itself. In this case, the computer doesn't care. He, as always, consistently executes the commands that he met from top to bottom.
If you remember mathematics, then there you can meet the principle of mathematical induction. It is as follows: some statement is true for every natural n if
1) it is valid for n = 1;
2) from the validity of the statement for any arbitrary natural n = k it follows that it is true for n = k+1.
In programming, this technique is called recursion.
Recursion is a way of defining a set of objects in terms of the set itself, based on given simple base cases.
Recursive is a procedure (function) that calls itself directly or through other procedures and functions.
Example of a recursive procedure:
void Rec(int a)
{
if (a>0) { Rec(a-1); }
Console.WriteLine(a);
}
Schematically, the work of recursion can be represented as a flowchart.
Rec() procedure is executed with parameter 3 Then, inside the procedure with parameter 3, the procedure with parameter 2 is called, and so on, until the procedure with parameter 0 is called. work. Then control is transferred back to the procedure with parameter 1, it also finishes its work by printing the number 1, and so on. before the procedure with parameter 3.
All called procedures are stored in memory until they complete their work. The number of concurrent procedures is called recursion depth.
|
We found out that recursion is the repeated execution of contained commands in a subroutine. And this, in turn, is similar to the work of the cycle. There are programming languages in which the loop construct is absent at all, for example, Prolog.
Let's try to simulate the work of the loop for.
The for loop contains a step counter variable. In a recursive subroutine, such a variable can be passed as a parameter.
// procedure LoopImitation() with two parameters
// first parameter – step counter, second parameter – total number of steps
static void LoopImitation(int i, int n)
{
Console.WriteLine("Hello N" + i); // statement to be repeated for any value i
if (i < n) // until loop counter equals n,
{
LoopImitation(i+1, n); // calling a new instance procedure, with parameter i+1 (go to the next i value)
}
}
|
Recursion and iteration
To understand recursion, you need to understand recursion...
Iteration in programming - one stepof a cyclic data processing process.
Often iterative algorithms at the current step (iteration) use the result of the same operation or action calculated at previous steps. One example of such calculations is the calculation of recurrence relations.
A simple example of a recursive value is the factorial: \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\).
The calculation of the value at each step (iteration) is \(N=N \cdot i\) . When calculating the value of \(N\), we take the already stored value \(N\).< br />
The factorial of a number can also be described using the recurrent formula:
\(\begin{equation*} n!= \begin{cases} 1 &\text{n <= 1,}\\ (n-1)! \cdot n &\text{n > 1.} \end{cases} \end{equation*}\)
You may notice that this description is nothing more than a recursive function.
Here the first line ( \(n <= 1\)) is the base case (recursion termination condition) and the second line is the transition to the next step. < br />
| Recursive factorial function |
Iterative algorithm |
static int Factorial(int n){
if (n > 1)
return n * Factorial(n - 1);
else return 1;
}
|
int x = 1;
for (int i = 2; i <= n; i++)
x = x * i;
Console.WriteLine("%d", x);
|
It should be understood that function calls involve some additional overhead, so a non-recursive factorial calculation will be slightly faster.
Conclusion: where you can write a program with a simple iterative algorithm, without recursion, then you need to write without recursion. But still, there is a large class of problems where the computational process is implemented only by recursion.
On the other hand, recursive algorithms are often more understandable.
|
Recursive translation of a number from one number system to another
In in some situations in procedures, you can use the word return without an argument - that is, in fact, the procedure still does not return anything. This can be useful when recursing, when return is used to end the descent at base cases of parameter values being recursed over. For example, a procedure that converts a number from decimal to binary may look like this:
static void printTwo(int n)
{
if (n == 0) return;
printTwo(n / 2);
if (n % 2 == 0) Console.Write(0);
else Console.Write(1);
}
|
Task
In the alphabet of the language of the tribe "Tumba-Yumba"; four letters: "K", "L", "M" and "N". You need to display all the words consisting of n letters that can be built from the letters of this alphabet.
The problem is a normal brute-force problem that can be reduced to a smaller problem.
We will sequentially substitute letters for the word.
The first position of a word can be one of the 4 letters of the alphabet (K. L, M, N).
Let's put the letter K first. Then, in order to get all variants with the first letter K, you need to enumerate all possible combinations of letters in the remaining n - 1 positions and so on. (see picture).
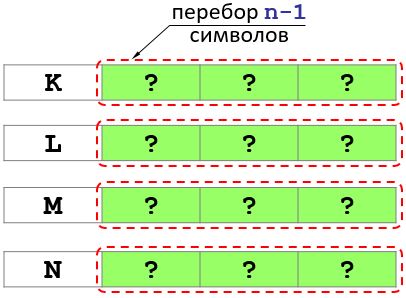 Thus, the problem is reduced to solving four problems of length n - 1.
Iterate over n characters recursively
w[0]='K'; // iterate over the last L-1 characters
w[0]='L'; // iterate over the last L-1 characters
w[0]='M'; // iterate over the last L-1 characters
w[0]='N'; // iterate over the last L-1 characters
w - a character string that stores the working word.
Thus, we got recursion. We can arrange the solution of the problem in the form of a recursive procedure.
It remains to determine when the recursion will end? When all characters are set, that is, the number of set characters is n. In this case, you need to display the resulting word on the screen and exit the procedure.
The C# program will look like this.
// w - changeable parameter (string-result)
// The TumbaWords procedure is passed the alphabet as a character string,
// the word word and the number of characters already set (at the beginning – 0)
static void TumbaWords( string A, ref string w, int N )
{
if (N == w.Length) // w.Length - the number of characters in the string
{
// if all characters have already been set to the word,
// then it is necessary to output a string and end the procedure
Console.WriteLine(w);
return;
}
for ( int i = 0; i < w.Length; i ++ ) // if the condition above is false (that is, not all characters are spaced,
{
// if the condition above is false (that is, not all characters are spaced,
// then in the loop we go through all the characters of the alphabet and
// alternately put the character on the first free space
w += A[i];
TumbaWords(A, ref w, N+1);
w = w.Remove(w.Length - 1); // and then remove the last added character,
// to make a new word with the same prefix
}
}
static void Main()
{
int n = Convert.ToInt32(Console.ReadLine());
string word = "";
TumbaWords("KLMN", ref word, 0);
}
NOTE that w is a mutable parameter (result string)!
|