Hashing

Error

Instead of just calculating the hash of a sequence, we can store the value at each of its prefixes. Note that these will be hash values ​​for sequences equal to the corresponding prefix.

With such a structure, you can quickly calculate the hash value for any subsegment of this sequence (similar to prefix sums).

If we want to calculate the hash of the subsegment [l;r], then we need to take the hash on the prefix r and subtract the hash on the prefix l-1 multiplied by p to the power of r-l+1. Why this is so becomes clear if you write the values ​​on prefixes and see what happens. I hope you succeed looking at this picture.



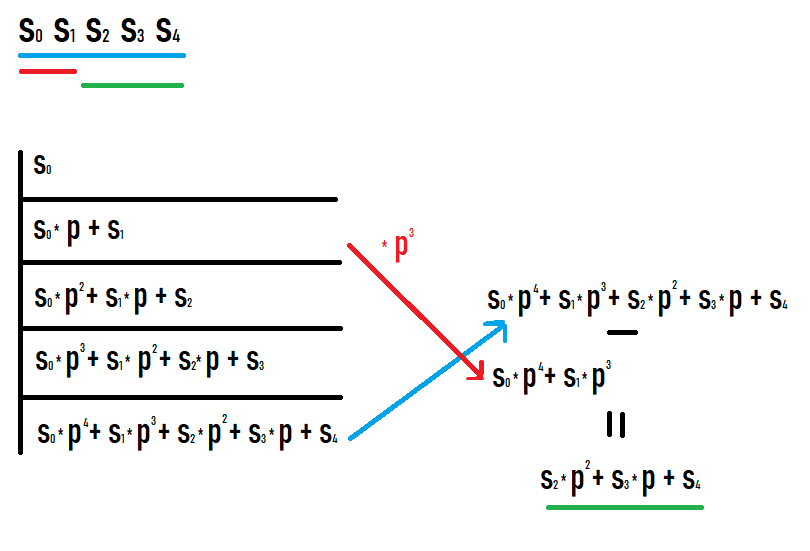
As a result of such actions, we get a hash of a subsegment of the original sequence. Moreover, this hash is equal to that if it were considered as a hash from a sequence equal to this subsegment (no additional conversions of degrees or the like are required to compare with other values).

There are two points to be clarified here:
1) To quickly multiply by p to the power r-l+1, it is necessary to precalculate all possible powers of p modulo mod.
2) It must be remembered that we perform all calculations modulo modulo, and therefore it may turn out that after subtracting the prefix hashes, we will get a negative number. To avoid this, you can always add mod before subtracting. Also, do not forget to take the modulo value after multiplications and all additions.

In code it looks like this:
  #include <bits/stdc++.h> using namespace std; typedef long longll; const int MAXN = 1000003; // base and hash module ll p, mod; // prefix hash and exponents p h[MAXN], pows[MAXN]; // calculating the hash of the subsegment [l;r] ll get_segment_hash(int l, int r) { return (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod; } int main() { // somehow get p and mod // precalculate powers p pows[0] = 1; for (int i = 0; i < MAXN; i++) pows[i] = (pows[i - 1] * p) % mod; // // main problem solution // return 0; }

If we have a hash of string A equal to h_A and a hash of string B equal to h_B, then we can quickly calculate the hash of string AB:
h_AB = h_A * p^|B| + h_B   <- counting everything modulo
where |B| - the length of the string B.

In addition to sequences, you can also hash sets. That is, sets of objects with no order on them. It is calculated according to the following formula:
hash(A) = \(\sum_{a \in A} p^{ord(a)}\)   <- counting everything modulo
where ord is a function that assigns to an object of the set its absolute ordinal number among all possible objects (for example, if the objects are natural numbers, then ord(x) = x, and if lowercase Latin letters, then ord('a' ;) = 1, ord('b') = 2 etc.)

That is, for each object we associate a value equal to the base to the power of the number of this object and sum up all these values ​​in order to obtain a hash of the entire set. As is clear from the formula, the hash is easily recalculated if an element is added to or removed from the set (just add or subtract the required value). Same logic,  if not single elements are added or removed, but other sets (just add / subtract their hash).

As you can already understand, single elements are considered as sets of size 1, for which we can calculate the hash. And larger sets are simply a union of such single sets, where by combining sets, we add their hashes.

In fact, this is still the same polynomial hash, but before the coefficient at p^m , we had the value of the sequence element under number n - m - 1 (where n is the length of the sequence), and now this is the number of elements in the set whose absolute ordinal number is equal to m.

In such hashing, one must take a sufficiently large base (larger than the maximum set size), or use double hashing to avoid situations where a set of p objects with absolute ordinal number m has the same hash as a set with one object with absolute ordinal number m+1.
 

There are also several ways to efficiently hash rooted trees. 
One of these methods is arranged as follows:
We process the vertices recursively, in order of traversal in depth. We will assume that the hash of a single vertex is equal to p. For vertices with children, we first run the algorithm for them, then through the children we will calculate the hash of the current subtree. To do this, consider the hashes of subtrees of children as a sequence of numbers and calculate the hash from this sequence. This will be the hash of the current subtree.
If the order on the children is not important to us, then before calculating the hash, we sort the sequence of hashes from the child subtrees and then calculate the hash from the sorted sequence.

This way you can check the isomorphism of trees - just count the hash without order on the children (that is, each time sorting the hashes of the children). And if the hashes of the roots match, then the trees are isomorphic, otherwise not.

For unrooted trees, everything happens in a similar way, but the centroid must be taken as the root. Or consider a pair of hashes if there are two centroids.