Kolobok left his grandmother and went to travel. Unexpectedly for himself, he wandered into the country of Evenland. The first difficulties stood in his way: Kolobok and the entrance to the country were separated by a huge moat with water, which, as you know, does not have a very good effect on our hero. Fortunately, there are air currents everywhere that could lift the one who stands on them to a certain height. The country is not just called Evenland, so all the heights to which air currents can raise the hero — they are even numbers.
Let's represent the air currents as an array h[1..n] of n natural numbers — flow heights. For every 1 ≤ i≤ n count G[i] — the index of the nearest element on the left that is strictly greater than h[i]. More formally, g[i] = max{j | j < i and h[j] > h[i]}. If i = 1 or there is no element greater than h[i] then G[i] is considered equal to 0.
Kolobok believes that the optimal location of air flows is determined by the sum
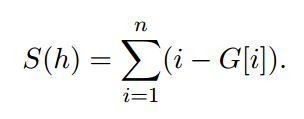
The smaller the amount, the better the location. Everything that Gingerbread Man can do now — this is to increase the height of one of the air streams by no more than m. After this action, the height of the flow should remain an integer, but can, if necessary, become odd.
Help Kolobok to make the optimal change, which will allow the sum S(h) described above to be minimal after the action.
Input file format
The first line of the input file contains numbers n, m (1 ≤ n ≤ 10
5 , 1 ≤ m ≤ 10
9 ) — the number of air flows and the maximum value by which you can increase the height of one of them. The second line gives the air flow heights h[i] (1 ≤ h[i] ≤ 10
9 ). It is guaranteed that all heights — even numbers.
Output file format
In a single line of the output file print a single integer — the minimum required amount.
|
Enter |
Output |
3 100
4 2 6
|
4 |
3 2
4 2 6
|
5 |
3 10
2 2 2
|
4 |