There are n planets in the galaxy, each of which is inhabited by many different living creatures. And each of them can be in trouble! Space rescuers are well aware of this and are always ready to help anyone who really needs this help. You just have to call.
Space rescuers are now planning to build the largest rescue base in the history of the galaxy, but the location of the future base has not yet been determined. Since help is sometimes required absolutely urgently, rescuers strive to find a point in the galaxy from which it would be possible to get to the most distant planet in the shortest possible time. In other words, it is necessary to find such a point in space so that the distance from it to the planet most distant from it is the smallest of all possible points in space. Unfortunately, they are unable to solve such a problem.
Because the planets are quite far apart, they can be thought of as points in Euclidean 3D space. Distance between points (x
i, y
i, z
i) and (x
j, y
j, z
j) is calculated by the formula:
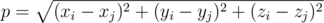
The rescue base can be located at any point in space, including coincidence with any of the planets.
The galaxy is in danger! Rescue the space rescuers and point them to the desired point.
Input
The first line of the input file contains an integer n — the number of planets (1 ≤ N ≤ 100). Each of the next n lines contains information about the planets. i-th of these lines contains three integers xi, yi, zi — i-th planet coordinates ( - 104 ≤ xi, yi, zi ≤ 104, 1.thinsp;≤ i ≤ n). No two planets are the same.
Output
In the first line of the output file, print three space-separated real numbers x
0, y
0, z
0 — base coordinates. If there are several solutions, then it is allowed to print any one. The answer will be counted if the distance from this point to the most distant planet differs from the result of the jury by no more than 10
-6 in absolute or relative value.
| Input |
Output |
|
5
5 0 0
-5 0 0
0 3 4
4 -3 0
2 2 -2
|
0.000 0.000 0.000 |