Peter creates a field for his new game. The field is divided into cells and is a rectangle measuring N on M cells. Let the cells have coordinates from 1 to N from left to right horizontally and from 1 to M from bottom to top vertically.
Peter has already placed a supermarket on this field, which is a rectangle of size C on D cells (C ;–– size horizontally, D –– vertically), and the bottom left cell of the supermarket has coordinates A, B on the playing field (see examples and pictures). Now Petya needs to place the stock exchange building on the same playing field. The stock exchange building is a rectangle measuring E on F cells (E –– horizontally, F –– vertically). Naturally, the exchange building should be completely located on the playing field and should not have common cells with a supermarket (but it can touch it).
In how many ways can Petya place the stock exchange building?
Input
Numbers are entered N, M, A, B, C, D, E, F, each on a separate line. The numbers satisfy the following conditions: 1 ≤ N ≤ 100, 1 ≤ M ≤&thinsp ;100, 1 ≤ A ≤ N, 1 ≤ B ≤ M, 1 ≤ A + C - 1&thinsp ;≤ N, 1 ≤ B + D - 1 ≤ M, 1 ≤ E ≤ N, 1 ≤ F ≤ M.
Imprint
Print the number of ways to place the stock exchange building.
| Input |
Output |
6
5
2
3
3
2
1
2 |
15 |
4
4
2
2
3
2
2
2
|
0 |
6
5
1
1
3
3
3
3 |
3 |
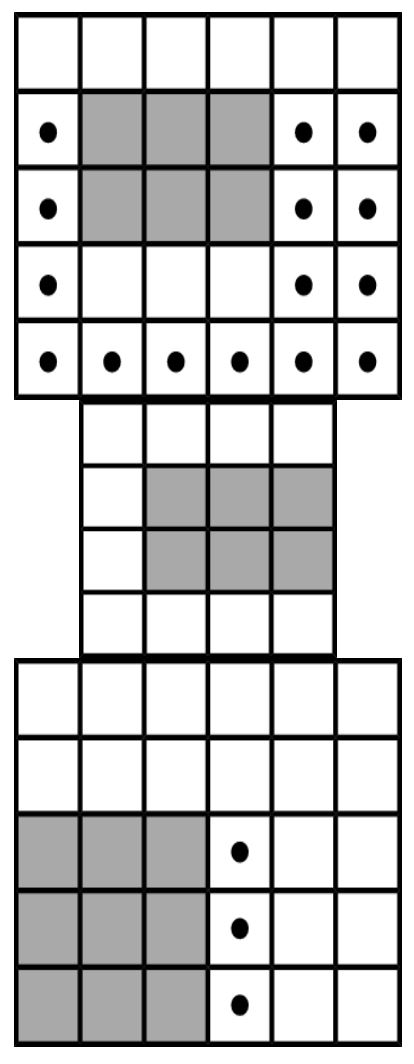
Note
The figures below correspond to the examples given. In the figures, the supermarket building is shown in gray. The dots mark the options for placing the lower left corner of the exchange building.