In football tactics, one of the basic concepts is the game scheme. It determines how many of the ten outfield players will play defense, how many — in midfield and how much — on the attack.
For example, a 5-3-2 formation means a team has five defenders, three midfielders, and two forwards. In accordance with modern concepts, the following restrictions are imposed on the game scheme: there must be at least one and no more than five defenders, at least one and no more than five midfielders and no more than three attackers. Note that the attackers may not be in the team at all. We will consider only such schemes.
We will assume that the football field has a length of 120 meters and a width of 80 meters. Let us introduce a rectangular Cartesian coordinate system on it in such a way as shown in the figure. The gates of the team we are considering are on the left.
We will also assume that a player is in the midfield line at some point in time if he is at a distance of no more than 20 meters from the center line. Accordingly, the player is in the line of defense if he is no more than 40 meters from "his" the front line, and in the attack line, if it is located no more than 40 meters from the "stranger" front line.
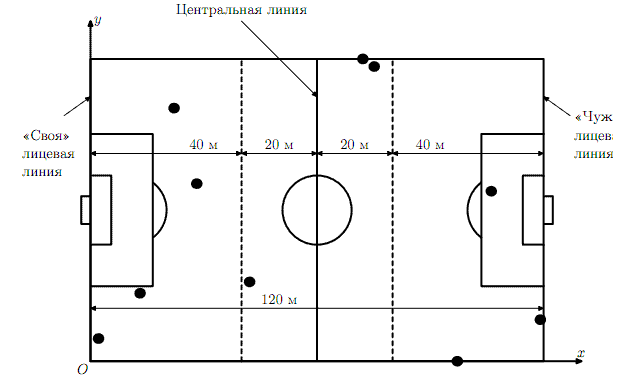
For example, in the situation shown in the figure, there are four players in the defensive line, in the midfield line — three, in the line of attack — also three.
During the game, some players can move from one line to another. In this problem, we assume that it is possible to move from midfield to defense (and vice versa) and from midfield to attack (and vice versa). Thus, a player who, in accordance with the scheme of the game, is a defender, cannot be in the offensive line, and vice versa — a player who, according to the scheme of the game, is an attacker, cannot be in the defensive line. In addition, in accordance with the instructions of the coach, no more than two players could move from each line to each.
Your task is to write a program that, given the positions of the players at some point in time, will find all possible game schemes under which such an arrangement of players could arise during the game.
Input
The input file contains ten lines containing two integers xi and yi each, — coordinates of each player on the team (0 ≤ xi ≤ 120, xi ≠ 40, xi ≠ 80, 0 &le ;yi ≤80).
Imprint
In the first line of the output file print k — the number of game formations a team can play. On the next k lines, in any order, print a description of each of these schemes. Follow the data format shown in the example.
Examples
| # |
Input |
Output |
| 1 |
97 0
13 18
26
119 11
42 21
72 80
75 78
106 45
22 67
28 47 |
9
2-5-3
3-5-2
3-4-3
4-5-1
4-4-2
4-3-3
5-4-1
5-3-2
5-2-3
|