Scientist Ivan Ivanovich studies inverted genealogies. An inverted pedigree is a set of people, each of whom either both of his parents are known, or none of the parents are known. In addition, it is known that all people from the pedigree have exactly one
a child, except for one person who has no children at all. Therefore, if we number people with integers from 1 to n, then we can denote by s
i the number of the child of person with number i and say that s
i = 0 in if the person with number i has no children.
We will assume that person a is included in the pedigree of person b, if either a = b, or if b has known parents, and a is included in the pedigree of one of the parents of b.
We will assume that a pedigree has been skewed with the participation of a certain person if both of his parents are known and the number of people in the pedigree of one of his parents is at least twice as large as the number of people in the pedigree of the second parent.
Ivan Ivanovich counted the number of distortions in the pedigree and got the number k, but, of course, he did it manually and could make a mistake. Help Ivan Ivanovich check his calculations: using numbers n and k, tell if there is a family tree of n people with k distortions, and if so, give an example of such a family tree.
Input data format
The single line contains two integers n and k (1 ≤ n ≤ 100 000, 0 ≤ k ≤ n) — the number of people in the pedigree and the number of distortions in it.
Output data format
In the first line print "YES" (without quotes) if there is a pedigree with n people and k skews, and "NO" (without quotes) otherwise.
If the required genealogy exists, then on the second line print n integers s1, s2, . . . , sn (0 ≤ s
i ≤ n) specifying the numbers of children of each of the n people in the family tree. If there are several desired pedigrees, print any one.
Examples
| # |
Input |
Output |
| 1 |
3 0 |
YES
0 1 1
|
| 2 |
5 1 |
YES
0 1 1 3 3
|
| 3 |
3 2 |
NO |
Remark
In the first example, the only pedigree that can be made up of three people (a person and his two parents) will do.
In the second example, the following pedigree would work:
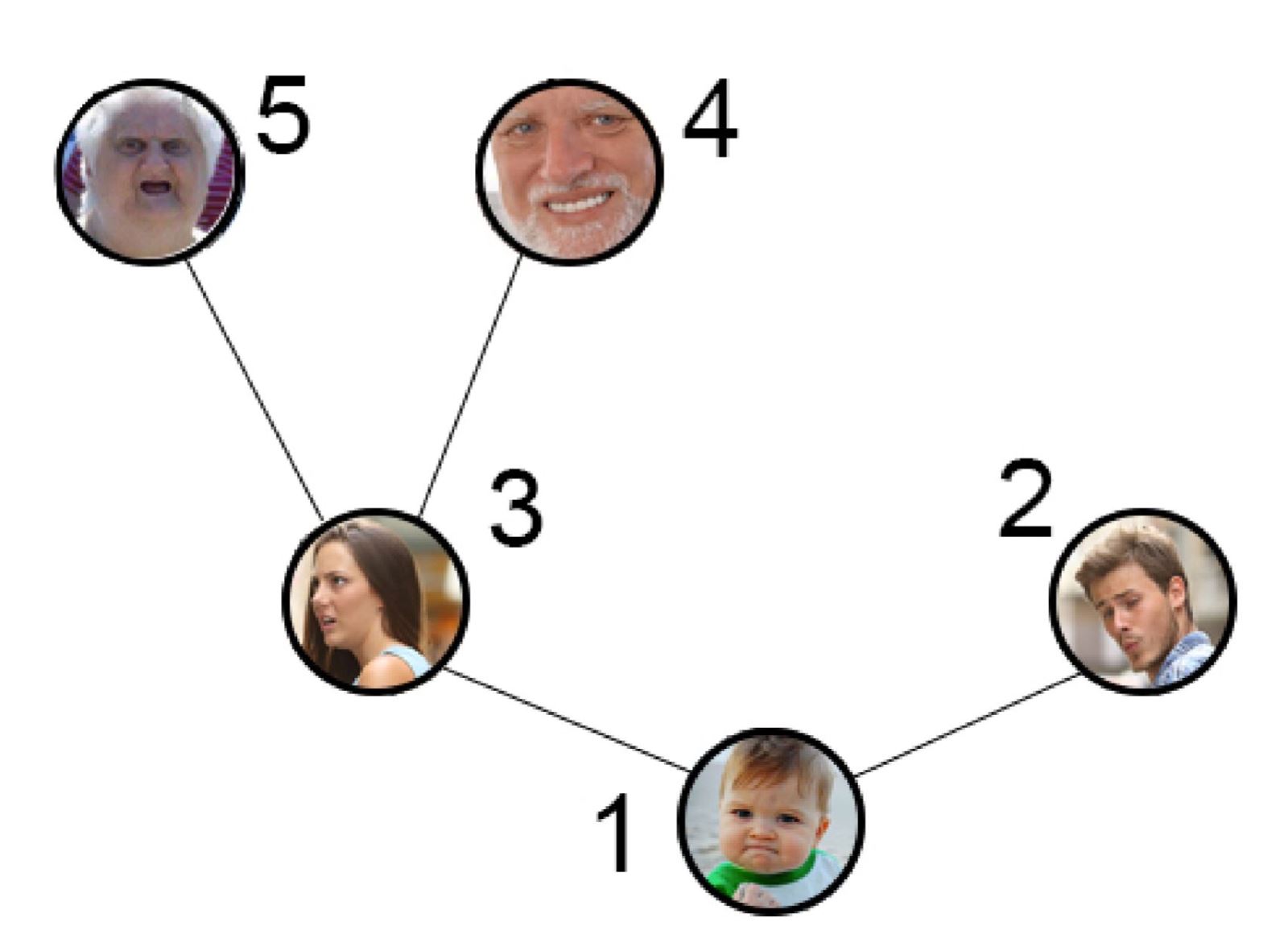
In this case, the pedigree of person 1 includes five people (people 1, 2, 3, 4, 5), the pedigree of person 2 includes one person (only 2), the pedigree of person 3 includes three people (3, 4, 5) , person 4's pedigree includes one person (only 4) and person 5's pedigree includes one
person (only 5). In this case, the pedigree is skewed in person 1.
In the third example, it can be shown that there is no pedigree of three people with two skews.