As you know, the most difficult thing when driving a car (on roads with right-hand traffic) is to turn left, because in this case you need to let cars moving towards you. Therefore, in a certain city, all left turns were banned, that is, at intersections, you can either continue moving in the same direction or turn right. It is forbidden to turn around and turn left at intersections.
The city plan is a rectangular grid, at the nodes of the grid there are intersections connected by roads. The distance between intersections is equal to 1. But some passages between intersections are closed, you can only move along white streets (including the outer white border), you can’t drive along gray streets and intersections.
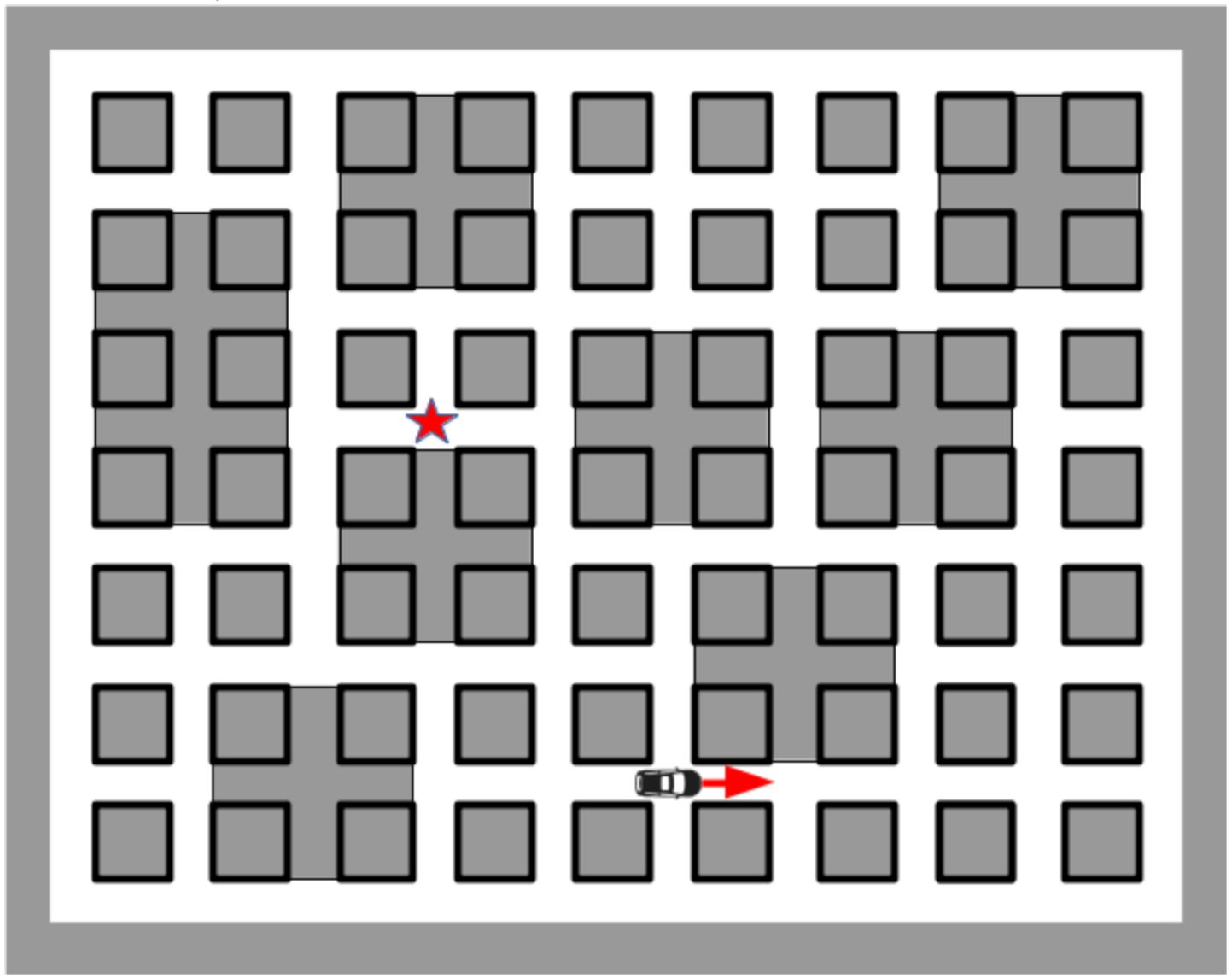
Your vehicle is at the intersection marked with the image of the vehicle and is moving in the direction of the arrow. That is, the next intersection at which the car can arrive is located in the direction of the arrow.
You need to come to the intersection marked with an asterisk. You can arrive at this intersection from any of the three possible directions.
Construct a car route of the shortest length that does not contain left turns.
The answer must be written as a sequence of integers, each number can take a value from 1 to 9. The number is equal to the number of blocks (gaps between intersections) that the car passes in the forward direction, then the car turns right.
For example, the sequence “4 1” means the car goes 4 blocks, turns right, then goes 1 block. In this case, the car will end up in the lower right corner of the map if it starts in the direction of the arrow.