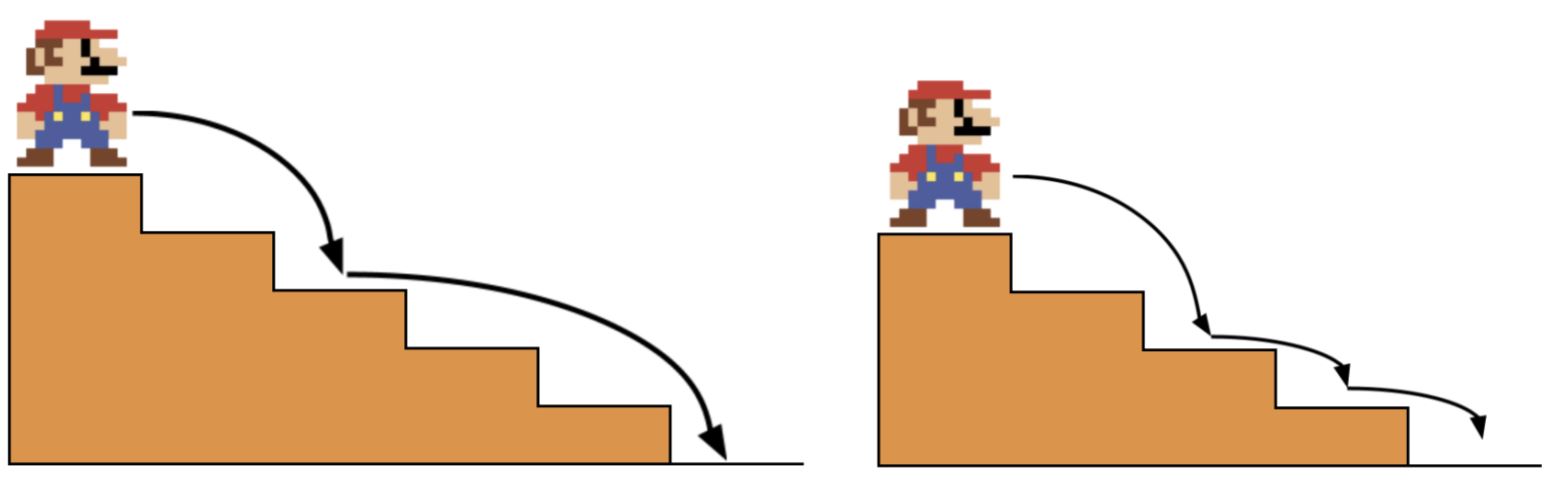
The character of the famous computer game Mario has grown old and almost stopped jumping. But just recently, he saw the descent of N steps, and he was covered with nostalgia. Mario stood on the highest step and decided to overcome this descent by jumping.
Once upon a time, Mario knew thousands of different types of jumps, but now he could only remember two: short and long. A short jump allows you to go down an arbitrary number of steps, no more than X, but a long — by an arbitrary number not greater than Y (X < Y ). But due to his age, Mario cannot make two long jumps in a row and is forced to make at least one short jump between them. At the same time, Mario does not want to worsen his past results too much and therefore will try to get by with as few jumps as possible.
Help Mario calculate the minimum number of jumps required to overcome all N steps.
Input
The first line of the input contains an integer X — maximum length of a short jump.
The second line contains an integer Y (1 ≤ X < Y ≤ 10
18) — the maximum length of a long jump.
The third line contains an integer N (1 ≤ N ≤ 10
18) — the number of steps in the descent.
Imprint
In a single line print an integer — the minimum number of jumps that Mario needs to descend.
Examples
| # |
Input |
Output |
| 1 |
2
3
5 |
2 |
| 2 |
1
2
4 |
3 |
| 3 |
1
100
1000000000000000000 |
19801980198019801 |
Remark
The images below show possible ways to solve the first two tests from the condition: