Given a rectangle of N x M squares. We call the squares on the border of the rectangle extreme. Let's call the distance from any square to the edge the number of moves that need to be made from the given square to the square adjacent to the side in order to get from this square to the extreme square. The squares with the maximum distance to the edge will be called central. In this case, the square can be both extreme and central at the same time.
The figure shows a rectangle for N = 7 and M = 8, in each square of which the distance from this square to the edge is recorded. This rectangle has two central squares.
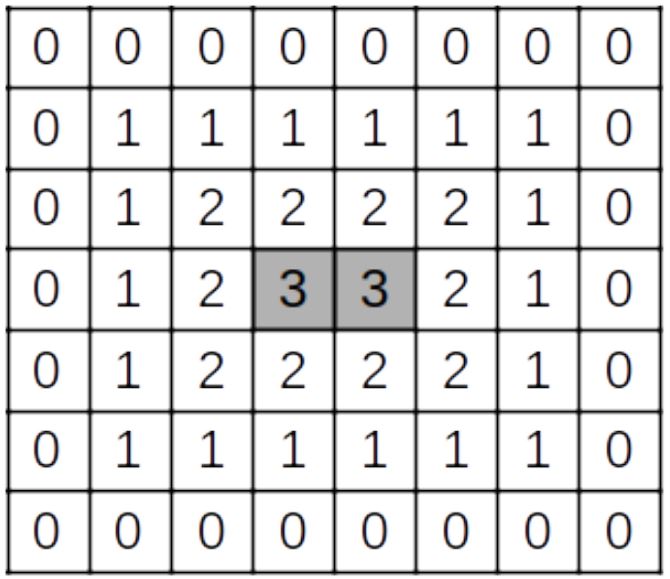
Given N and M, determine the number of central squares in the rectangle.
Examples