|
Темы:
Recurrent sequences
Besi has N (3≤N≤40) favorite points on a 2D lattice, no three of which are collinear. For each 1≤i≤N, the i-th point is given by two integer coordinates xi and yi (0≤xi,y< sub>i≤104).
Besi draws some lines between the points like this:
It selects some permutation p1,p2,…,pN from N points
It draws segments between p1 and p2, p2 and p3, p3< /sub> and p1.
Then for each integer i from 4 to N in order, it draws line segments from pi to pj for all j<i so that this line segment does not intersect any of the previously line segments drawn (outside endpoints)
Besi noticed that for each i, she drew exactly three new segments. Calculate the number of permutations Besi could have chosen in step 1 that satisfy this property modulo 109+7.
Input:
The first line contains N.
Each of the following N lines contains two space-separated integers xi and yi.
Output:
Number of permutations modulo 109+7.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
4
0 0
04
1 1
1 2
| 0 |
No swapping will work. |
| 2 |
4
0 0
04
40
1 1
| 24 |
All permutations work. |
| 3 |
5
0 0
04
40
1 1
1 2
| 96 |
One of the permutations that satisfies the property - (0,0),(0,4),(4,0),(1,2),(1,1).
For this permutation
- First, it draws lines between each pair of (0,0),(0,4), and (4,0).
- It then draws lines from (0.0), (0.4), and (4.0) to (1.2).
- Finally, it draws lines from (1,2), (4,0), and (0,0) to (1,1).
Pattern:
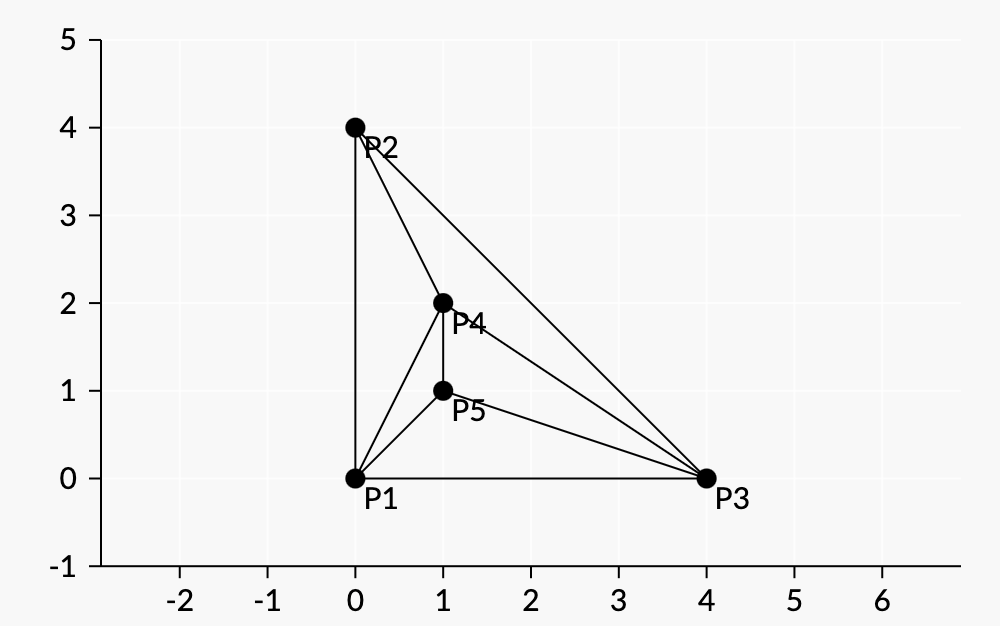
A permutation does not satisfy a property if its first four points are (0,0)(0,0), (1,1)(1,1), (1,2)(1,2), and (0,4)(0,4) in some order. |
|