| Problem description | | Progress |
|
Темы:
Dynamic Programming: One Parameter
The grasshopper jumps on columns located on the same line at equal distances from each other. The columns have serial numbers from 1 to N . At the beginning, the Grasshopper sits on a post with the number 1. It can jump forward from 1 to K bars, counting from the current one.
On each column, the Grasshopper can gain or lose several gold coins (this number is known for each column). Determine how the Grasshopper needs to jump in order to collect the most gold coins. Keep in mind that the Grasshopper cannot jump backwards.
Input:
- the first line contains two natural numbers: N and K (\(2 <= N ,\ K < = 10000\)), space-separated;
- in the second line, space-separated N-2 integers – the number of coins the Grasshopper gets on each column, from 2nd to N-1th. If this number is negative, the Grasshopper loses coins.
It is guaranteed that all numbers in modulo do not exceed 10000.
Output:
- in the first line, the program should display the maximum number of coins that the Grasshopper can collect;
- the second line displays the number of Grasshopper's jumps;
- on the third line – numbers of all columns visited by the Grasshopper (separated by a space in ascending order).
If there are several correct answers, print any of them.
Examples
| # |
Input |
Output |
| 1 |
5 3
2 -3 5
|
7
3
1 2 4 5
|
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
The grasshopper jumps on columns located on the same line at equal distances from each other. The columns have serial numbers from 1 to N . At the beginning, the Grasshopper sits on a post with the number 1. It can jump forward from 1 to K bars, counting from the current one. It is required to find the number of ways in which the Grasshopper can get to the column with the number N. Keep in mind that the Grasshopper cannot jump backwards.
Since the number of ways to find can be very large, modulo \(10^6 + 7\) , i.e. find the remainder of the division this number to \(10^6 + 7\) .
Input: The input string contains natural numbers N and K separated by a space. It is guaranteed that \(1 <= N ,\ K <= 10000\).
Output: The program should print a single number: the number of ways the Grasshopper can get to the column numbered N calculated from module \(10^6+7\).
Examples
| # |
Input |
Output |
| 1 |
10 5 |
236 |
| 2 |
100 50 |
934384 |
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
Carnations are driven into a straight plank. Any two cloves can be connected with a thread. It is required to connect some pairs of studs with threads so that at least one thread is tied to each stud, and the total length of all threads is minimal.
Input:
- the first line contains the number N - the number of studs (\(2 <= N <= 100\));
- the next line contains N numbers - the coordinates of all the studs (non-negative integers, not exceeding 10000).
Output: print a single number - the minimum total length of all threads.
Examples
| # |
Input |
Output |
| 1 |
5
4 10 0 12 2
|
6 |
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
A line of N people lined up for tickets to the premiere of the new musical, each of whom wants to buy 1 ticket. Only one ticket office worked for the entire queue, so ticket sales were very slow, bringing "guests" queues in desperation. The smartest ones quickly noticed that, as a rule, a cashier sells several tickets in one hand faster than when the same tickets are sold one at a time.
Therefore, they suggested that several standing people in a row give money to the first of them so that he buys tickets for everyone.
However, in order to fight speculators, the cashier sold no more than 3 tickets per person, so only 2 or 3 people in a row could reach an agreement in this way.
It is known that the cashier spends Ai seconds to sell one ticket to the i-th person in the queue, and Bi seconds to sell two tickets , three tickets - Ci seconds. Write a program that will calculate the minimum time that all customers could be served.
Note that tickets for a group of united people are always bought by the first of them. Also, no one buys extra tickets (that is, tickets that no one needs) in order to speed up.
Input:
- the first line contains the number N - the number of buyers in the queue (\(1<=N<=5000\));
- next comes N triples of natural numbers Ai, Bi, Ci. Each of these numbers does not exceed 3600. People in the queue are numbered starting from the cashier.
Output: print a single number - the minimum time in seconds that all customers could be served.
Examples
| # |
Input |
Output |
| 1 |
5
5 10 15
2 10 15
5 5 5
20 20 1
20 1 1
|
12 |
| 2 |
2
3 4 5
1 1 1
|
4 |
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
The Chess Association decided to equip all its employees with such telephone numbers that would be dialed on a push-button telephone with a knight's move. For example, the knight's move calls 340-4927. At the same time, the phone number cannot begin with either the number 0 or the number 8.
The phone keyboard looks like this:
Write a program to determine the number of telephone numbers of length N dialed by the knight.
Input: Input is an integer N (\(1< =N<=50\)).
Output: output the number of phone numbers you are looking for.
Examples
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
Simple games
There are N stones on the table. During a move a player can take:
- 1 or 2 stones if N is divisible by 3;
- 1 or 3 if N when divided by 3 gives remainder one;
- 1, 2 or 3 if N when divided by 3 leaves a remainder of two.
Each move can be made if there are enough stones. The one who cannot make a move loses.
Input: Enter an integer \(0 < N <= 100\).
Output: print 1 or 2 – the number of the player who will win if played correctly.
Examples
| # |
Input |
Output |
| 1 |
1 |
1 |
| 2 |
3 |
2 |
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
 Slinky< /strong> — a spring toy created in 1943 in the USA by Richard James In our country it was simply called Rainbow. All the children loved to launch her down the stairs, counting who would take her down. Slinky< /strong> — a spring toy created in 1943 in the USA by Richard James In our country it was simply called Rainbow. All the children loved to launch her down the stairs, counting who would take her down.
Usually "Rainbow" in the hands of the children, it went down to the next step, to the step after one or after 2. (For example, if Rainbow was launched from the 10th step, then it could stop on the 9th, 8th or 7th.)< br />
Let's say there are N steps on the stairs. Determine the number of possible "routes" Rainbows from the top of the stairs to the ground.
Input
A single number is entered \(0 < N < 31\).
Output
Print a single number — number of "routes" Rainbows.
Examples
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
Caring owners of the apartment take care of the cockroach Vasily. In the evening they lay out a row of N breadcrumbs for him, which he loves very much. Passing from one bread crumb to another, the cockroach Vasily may or may not eat it. But he never eats two breadcrumbs in a row.
Count how many different options for eating bread crumbs the cockroach Vasily has.
Input
The program input an integer N (\(1<=N<=100\) ).
Output
Print the answer to the problem.
Examples
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
Once upon a time in childhood, we all enjoyed playing the game "Pebbles" or "Five pebbles", as someone called it. For the game, ordinary pebbles were needed, which could easily be found on the street. It was possible to play anywhere;
The first step of the game was as follows. All five pebbles are thrown to the ground in front of them. One of them was chosen. This is a cue ball. This pebble is thrown into the air and while it flies, it is necessary to pick up one of the pebbles remaining on the ground and have time to catch the flying one with the same hand. The picked up pebble is set aside and the action is repeated for all remaining pebbles.
In the following steps, the number of pebbles to pick up increases. The last step was the exam, when it was necessary to throw all the collected pebbles into the air and catch them with the back of the hand, and then toss again and catch them with the open palm. How many pebbles in the end remained, so many points you get. The turn passes to the next player, who also repeats all the steps. Then a new round of the game was launched. The winner was the one who scored the most points for all rounds.
A lot of guys made the game difficult in all sorts of ways.
Let's say the guys have an infinite number of pebbles lying on the ground. At the end of the round, they do not need to catch all the pebbles in their palms, but exactly enough so that their total number of points increases by 1 or doubles or triples. Before the start of the game, everyone already has 1 point. The winner will be the one who gets N points faster.
Let's assume that all players have enough playing experience, and they always reach the exam with the number of stones they need (so that they can increase the required number of points by 1, double or triple).
Determine the minimum number of rounds you need to play in order to get the given number of points N from 1 .
Input
The program receives a single number as input, not exceeding 106.
Output
You need to print one number: the least number of operations you are looking for.
Examples
| # |
Input |
Output |
| 1 |
1 |
0 |
| 2 |
5 |
3 |
| 3 |
32718 |
17 |
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
Binary search in an array
The spacebar does not work on Vasya's keyboard. Therefore, he is now typing all the texts together. Write a program that will split the text typed by Vasya into words from the given dictionary.
Input
First, the input of the program receives the text entered by Vasya – one line of no more than 100 Latin lowercase letters. The next input line specifies the value N – the number of words in the dictionary (N – is a natural number not exceeding 2000). The next N lines contain words from the – one word per line, each word contains no more than 20 Latin lowercase letters. The words are written in alphabetical order.
Imprint
Print Vasya's text with spaces between words (a space after the last word is acceptable). If there are several options for splitting the string into words, print any of them. It is guaranteed that at least one way to split a string into dictionary words exists.
Examples
| # |
Input |
Output |
| 1 |
whatcanido
6
a
an
can
do
i
what |
what can i do |
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
The popularity of the district Olympiad in Informatics is growing year by year. At the same time, the organizers must print out in advance both the conditions of the tasks and other materials of the Olympiad (questionnaires, memos, etc.). This year they estimated the volume of printed matter at N sheets.
A company that is ready to reproduce printed materials offers the following financial terms. She prints one sheet for A1 rubles, 10 sheets — for A2 rubles, 100 sheets — for A3 rubles, 1000 sheets — for A4 rubles, 10 000 sheets — for A5 rubles, 100 000 sheets — for A6 rubles and 1 000 000 sheets — for A7 rubles. However, it is not guaranteed that one sheet in a larger order will cost less than in a smaller one. And it may even turn out that it will be beneficial for any party to use the tariff for one sheet.
The printing of a specific order is made either by a combination of several tariffs, or by ordering a larger batch. For example, 980 sheets can be printed by ordering 9 batches of 100 sheets plus 8 batches of 10 sheets, 98 orders of 10 sheets, 980 orders of 1 sheet, or ordering 1000 (or even 10 000 or more) sheets if that is will be more profitable.
It is required to determine the minimum amount of money in rubles, which will be enough to fulfill the order, based on the given volume of the order in N sheets.
Input
The input to the program is first given the number N (1 ≤ N ≤ 2 × 109) — the number of sheets in the order. The next 7 input lines contain natural numbers A1, A2, A3, A4, A5, A6, A7 respectively (1 ≤ Ai ≤ 106).
Imprint
Print one number — the minimum amount of money in rubles that is needed to complete the order. It is guaranteed that the correct answer will not exceed 2 × 109.
Examples
| # |
Input |
Output |
| 1 |
980
1
9
90
900
1000
10000
10000
| 882 |
| 2 |
980
1
10
100
1000
900
10000
10000
| 900 |
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
Petya, studying how the exchange rate of the ruble changes against the dollar and the euro, deduced the law according to which these changes take place (or thinks he has deduced it). According to this law, Petya calculated what the exchange rate of the ruble would be against the dollar and the euro in the next N days.
Petya has 100 rubles. On each day, he can exchange currencies for each other at the current rate without limiting the number (at the same time, the dollar exchange rate against the euro corresponds to the value that can be obtained by exchanging the dollar for rubles, and then these rubles — for euros). Since Petya will operate not with cash currency, but with a bank account, he can perform exchange operations with any (including non-integer) number of units of any currency.
Write a program that calculates the maximum number of rubles Petya can get by the end of the N-th day.
The laws of rate changes are arranged in such a way that during the specified period the ruble equivalent of the amount that Petya may have will not exceed 108 rubles.
Input
The first line of the input file contains one number N (1≤N≤5000). Each of the next N lines contains 2 numbers calculated according to Peter's laws for the corresponding day — how many rubles will cost 1 dollar, and how many rubles will cost 1 euro. All these values are not less than 0.01 and not more than 10000. The values are specified exactly and are expressed as real numbers with no more than two decimal places.
Imprint
In the output file, output the desired value with an accuracy of at least two decimal places.
Examples
| # |
Input |
Output |
| 1 |
1
30.00 9999.99
| 100.00 |
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
Dynamic programming
Segment tree, RSQ, RMQ
Fenwick tree
Let's call a subsequence of array a a non-empty array b such that it can be obtained from array a by deleting some (possibly none) elements of array a. For example, array [1,3] is a sequence of array [1,2,3] , but [3,1] is not.
Let's call a subsegment of array a a non-empty array b such that it can be obtained by deleting several (possibly none) of the first and last elements of array a. For example, [1,2] is a subsegment of the array [1,2,3] , but [1,3] is not. It is easy to see that an array of length n has exactly \( {n(n+1) \over 2}\) subsegments.
Let's call an array a of length n increasing if for any 1 ≤ i≤ n ai ≤ ai+1.
The monotonicity of an array is the number of its increasing subsegments.
Given an array a of length n. Calculate the sum of monotonicities over all its subsequences. Since the answer can be very large, print it modulo 109+7.
Input
The first line contains an integer n (1 ≤ n ≤ 200000) — array length a.
The second line contains n integers (1 ≤ ai ≤ 200000) — array elements a.
Imprint
Print a single integer — the sum of the monotonicities of all subsequences modulo 109+7.
Note
In the first test case, the array has 7 subsequences:
- Array [1] has exactly one subsegment and is ascending.
- The array [2] has exactly one subsegment and is increasing.
- The array [3] has exactly one subsegment and is increasing.
- The array [1,2] has three subsegments ([1], [2], [1,2] ) and they are all increasing.
- The array [1,3] has three subsegments ([1], [3], [1,3] ) and they are all increasing.
- The array [3,2] has three subsegments ([3], [2], [3, 2] ), but only two of them ([3] and [2] ) are ascending.
- The array [1,3,2] has six subsegments ([1], [3], [2], [1,3], [3,2], [1,3,2] ) and four of them ([1], [3], [2], [1,3] ) are increasing.
In the second test case, all increasing subsegments of all subsequences have length 1.
Examples
| # |
Input |
Output |
| 1 |
3
1 3 2
| 15 |
| 2 |
3
6 6 6
| 12 |
| |
![]()
|
ID 38552.
hike
Темы:
Dynamic Programming: One Parameter
A group of schoolchildren decided to go camping along the Moscow River. The Moskva River has many tributaries that can flow into it both from the right and from the left bank.
The students want to start the hike at some point on the left bank and end the hike at some point on the right bank, possibly crossing the rivers several times. As you know, crossing both a river and a tributary is a certain difficulty, so they want to minimize the number of crossings made.
The schoolchildren studied the map in advance and wrote down the sequence in which tributaries flow into the Moscow River along their entire route.
Based on the given description of the tributaries, help the students determine the minimum number of crossings they will have to make during the trip.
Input
The only line contains a description of the Moskva River between the start and end points of the hike. The string length does not exceed 105 characters.
Each character of the string can be one of three Latin letters L, R or B. The letter L means that the next tributary flows into the river from the left bank, R - the tributary flows into the river from the right bank and B - the tributaries flow from both banks of the river in one place. The hike starts on the left bank before the described part of the river and ends on the right bank after the described part.
Imprint
Print one integer - the minimum number of crossings.
Notes
Drawing for the example below.
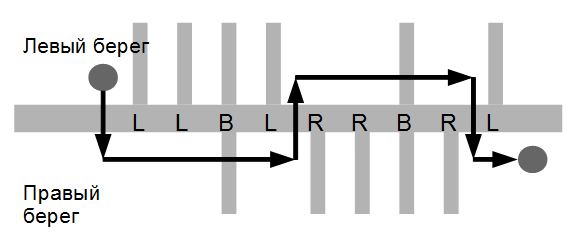
Examples
| # |
Input |
Output |
| 1 |
LLBLRRBRRL |
5 |
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
Consider a figure similar to the one shown in the figure (a large equilateral triangle made up of small equilateral triangles). The figure shows a figure consisting of 4 levels of triangles.
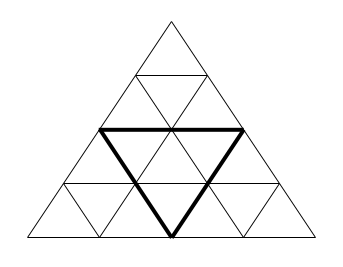
Write a program that will determine how many triangles there are in total (it is necessary to take into account not only "small" triangles, but in general all triangles — in particular, the triangle in bold, as well as the whole figure, are triangles of interest to us).
Input
Enter one number N — number of levels in the figure (1 ≤ N ≤ 100000).
Imprint
Print the number of triangles in such a figure.
Examples
| # |
Input |
Output |
| 1 |
1 |
1 |
| 2 |
2 |
5 |
| 3 |
4 |
27 |
| |
![]()
|
|
Темы:
Arrays
Prefix sums(minimums, ...)
Dynamic Programming: One Parameter
We have a grid with H rows and W columns. The square in the ith row and jth column will be called Square(i, j). Integers from 1 to H·W are written over the entire grid, and an integer written in Square(i, j) is equal to Ai,j.
You are a wizard and can teleport a shape placed on Square(i, j) to Square(x, y) by spending \(|x-i|+|y-j|\) magiks (magic coins).
Now you need to pass Q practice tests on your abilities as a wizard (sorceress). Ith test will be conducted as follows:
- initially the figure is located in the square, where the integer is written Li;
- Let x be the integer written in the square occupied by the shape. Repeatedly move the shape to the square where the integer x+D is written until x will not become equal to Ri. The test ends when x = Ri .
It is guaranteed that Ri- Li is divisible by D.
For each test, find the sum of magics consumed during that test.
Input
The first line contains three integers: H, W and D (\( 1\leq H,W \leq 300\), \(1 \leq D \leq H \cdot W\)).
The following H lines contain W numbers Ai,j (\(1 \leq A_{i,j} \leq H \cdot W\), \(A_{i,j} \ neq A_{x,y} ((i,j) \neq (x,y))\).
The next line contains an integer Q (\(1 \leq Q \leq 10^5\)).
The last Q lines contain 2 integers each: Li and Ri (\(1 \leq L_i \leq R_i \leq H \cdot W\)), \((R_i-L_i)\) multiple of D.
Imprint
For each test, print the sum of magics spent during this test. The output should be in the order of the tests.
Examples
| # |
Input |
Output |
Explanations |
| 1 |
3 3 2
1 4 3
2 5 7
8 9 6
1
48 |
5 |
- 4 is written as Square(1,2).
- 6 is in Square(3,3).
- 8 is written in Square (3,1).
Thus, the sum of magic points spent during one test is:
\((|3-1|+|3-2|)+(|3-3|+|1-3|)=5\).
|
| 2 |
4 2 3
37
14
5 2
68
2
2 2
2 2 |
0
0 |
Note that there may be a test where the shape doesn't move at all, and there may be multiple identical tests. |
| 3 |
5 5 4
13 25 7 15 17
16 22 20 2 9
14 11 12 1 19
10 6 23 8 18
3 21 5 24 4
3
13 13
2 10
13 13
| 0
5
0 |
|
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
To make it difficult to withdraw money, a bank on the planet Krokrys only allows its customers to withdraw one of the following amounts per transaction:
- 1 kroratcoin (a valid coin on the planet Krorat);
- 6 Croratscoins, 36 (=62) Croratscoins, 216(=63) Croratscoins , ...;
- 9 Croratscoins, 81 (=92) Croratscoins, 729(=93) Croratscoins , ...
What is the minimum number of operations required to output exactly N kroratcoins?
It is not possible to re-deposit the money you have withdrawn.
Input
The input is an integer N (\(1<=N<=100000\)).
Imprint
Output the answer to the problem.
Examples
| # |
Input |
Output |
Explanations |
| 1 |
127 |
4 |
If you withdraw 1 + 9 + 36 + 81, you will withdraw 127 kroratcoins in 4 operations. |
| 2 |
3 |
3 |
1+1+1 = 3, total 3 operations |
| 3 |
44852 |
16 |
|
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
Recurrent sequences
At the top of the ladder, which contains N stairs, there is a ball that starts jumping down them to the base. The ball can jump to the next step, to the step after one or after 2. (That is, if the ball lies on the 8th step, then it can move to the 5th, 6th or 7th.) Determine the number of possible " ;routes" ball from the top to the ground.
Input
Enter a single number 0 < N < 31.
Output
Print a single number — number of routes.
Examples
| |
![]()
|
|
Темы:
Dynamic Programming: One Parameter
Gromozeka's favorite chess piece is the rook. But he likes to walk her only vertically, and either one cell or two. Gromozeka ends the game when the rook reaches the end of the file. Thinking about the next position, he noticed that some cells on the path of the rook are under attack from the opponent's pieces and it is impossible to move on these cells.
Help Gromozeka calculate in how many ways he can move his rook to the other end of the chessboard without hitting the squares under attack.
Input
The first line contains one natural number N (N <= 40): the size of the chess field. The second line contains one natural number K (K <= N ): the number of cells under attack. The third line contains K different natural numbers in the range from 1 to N: the numbers of the squares under attack by the opponent's pieces.
Imprint
Output one number - the number of ways to get to the end of the vertical (to the N-th cell).
Examples
| # |
Input |
Output |
| 1 |
7
2
3 5
| 2 |
| 2 |
10
3
5 1 2
| 0 |
| 3 |
3
1
2 |
1 |
| |
![]()
|